どうも！宇宙ヤバイch中の人のキャベチです。

今回は「宇宙の形は３次元のドーナツ状だった！？」というテーマで動画をお送りしていきます。

平坦な宇宙

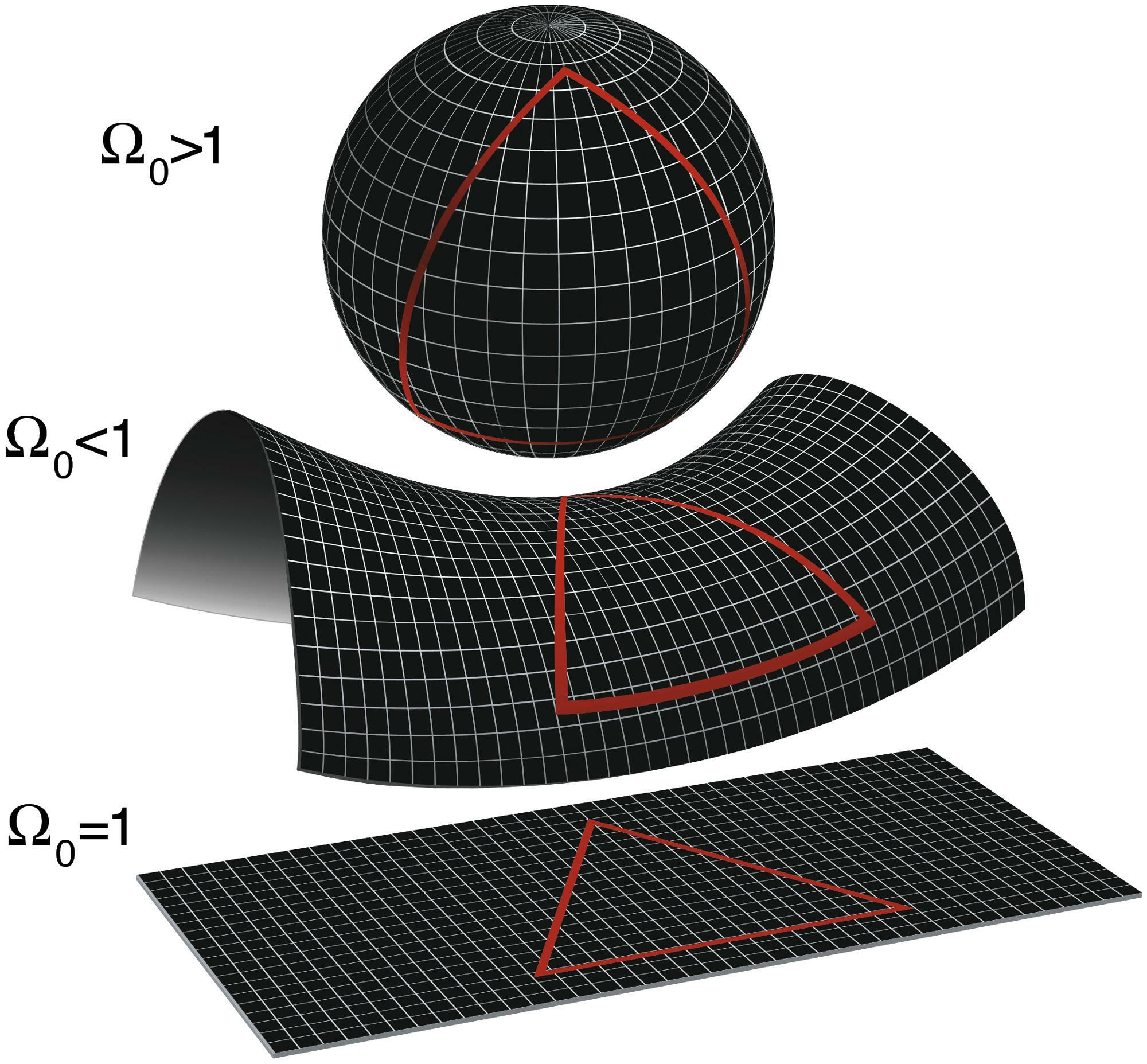
まず初めに、宇宙空間の曲がり方を表す量として曲率について紹介します。

宇宙は3次元ですが、次元を1つ落として2次元で考えてみると、2次元の曲面は曲率によって3パターンに分けることができます。

上の画像一番下の図のように曲率がゼロの場合、完全に平らな平面です。

平面では、三角形の内角の和は180です。

画像一番上のように曲率がプラスの場合、どの方向にも同じ様に曲がっている状態で、球面のように閉じた曲面になります。

この曲面では三角形の内角の和は180より大きくなります。

画像真ん中のように曲率がマイナスの場合、シートの方向によって曲がる向きが異なります。

馬の鞍のような形になります。

この曲面では三角形の内角の和は180より小さくなります。

この性質は私たちが住む3次元空間でも同じことが言えます。

科学者は、誕生から1億年後（1億歳）の宇宙の大きさを底辺、現在の地球をもう一つの頂点として三角形を設定して、その幾何学的な性質を調べました。

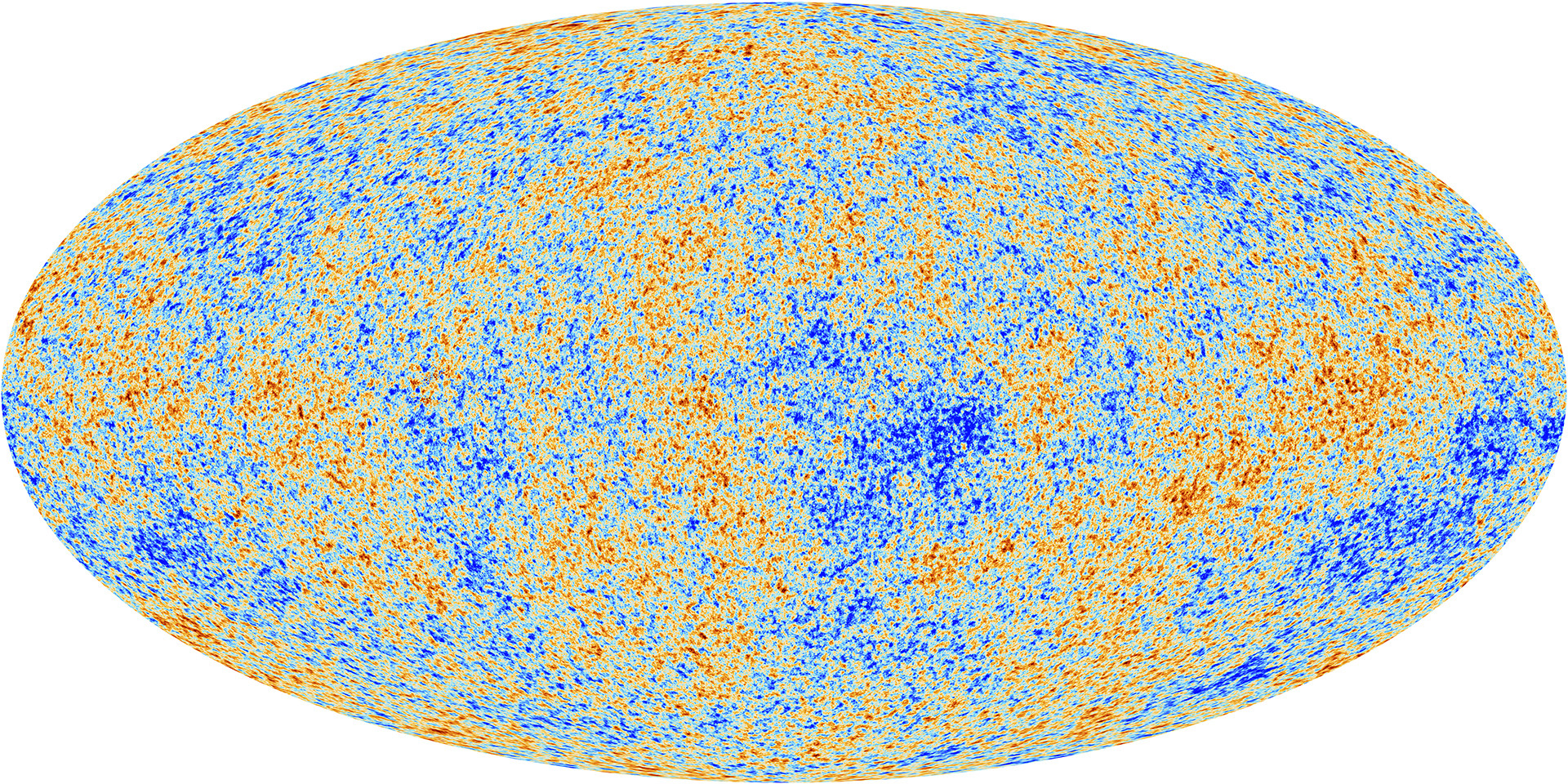
1億歳の宇宙についての情報は宇宙背景放射から得ることができます。

観測の結果、巨大な三角形はこの宇宙が平坦な宇宙であることを示す性質だったため、現在ではこの宇宙は平坦な宇宙である可能性が高いと考えられています。

平坦なドーナツ型とは

宇宙が平坦であれば、その空間には果てがなく、どこまでも行けてしまいそうです。

ですが実は平坦な宇宙でも大きさが有限な場合が考えられるのです。

今回も空間が2次元である場合を考えましょう。

まず、平面上に長方形（もしくは正方形）を描きます。

そして、その長方形の向かい合った辺を同じものとみなします。

つまり、上の辺と下の辺はつながっていて、右の辺と左の辺もつながっているのです。

実際に長方形の端と端をつなぐとどんな形になるでしょうか？

長方形は伸縮・変形が自在なゴムシートのようなものでできているとします。

まず、長方形の左右の辺を貼り合わせます。

するとできるのは円柱の側面です。

この円柱をグイッと曲げ伸ばして上下の辺をくっつけます。

するとドーナツの形になります。

このような形を数学的には「トーラス」といいます。

残念ながら、3次元空間の中では全ての点で曲率が0の平坦なトーラスを作ることはできません。

外側ではどの方向を見ても同じように曲がっているためプラスの曲率、内側では方向毎に曲がりの方向が異なるためマイナスの曲率になってしまいます。

実は、平坦なトーラスは、４次元以上の空間の中でしか実現できないのです。

４次元空間の中での平坦なトーラスの作り方については、非常に難しいのでここでの解説は割愛します。

詳細な解説がある外部リンクはこちら

まとめると、この宇宙が同じ平坦な宇宙であっても、ただ延々と空間が広がっている宇宙とは限らず、その形の候補の一つとして３次元の平坦トーラス型の宇宙が存在する、というわけです。

平坦なトーラス世界の特徴

それではいきなり実際の宇宙と同じ3次元の話をする前に、話を簡単にするため、まずは再び2次元の平坦トーラスの中での物体の動きを考えてみましょう。

平面上のトーラスの実体は長方形でした。

ただし、上の辺と下の辺はつながっていて、右の辺と左の辺もつながっているという状態の長方形でした。

この長方形の中に二次元の人がいるとすると、真ん中から左の端まで行ってさらに進むと右の端から出てくることになります。

上の端まで行ってさらに進むと下の端から現れます。

パックマンのような昔のアーケードゲームや、僕も大好きなドラゴンクエストのようなRPGの世界はこんな感じになっていることがよくあります。

実は多くのゲームではトーラス状の世界となっていたわけです。

では話を2次元から、実際の宇宙と同じ3次元へと戻します。

3次元の平坦トーラスは具体的な形をイメージするのが難しいですが、その中での物体や光の動きを考えることはできます。

例えば天井や床を含めて、隣り合う6つの面全てが別の部屋に繋がっている直方体の部屋があったとしましょう。

どの方向でもいいので部屋を出ると、そこは元の部屋と寸分違わず全く同じ部屋なのです。

2次元のRPGの世界と似ていますね。

隣の部屋を見てみると、自分の後ろ姿が何人も無限に連なって見えます。

つまり、左右の部屋も上下の部屋も前後の部屋も全て今いる部屋と同じで、どの部屋にも自分自身が居るのです。

このように３次元のどの方向にも同じ構造がループしているのが、3次元の平坦トーラスの世界です。

宇宙が平坦なトーラス型である証拠!?

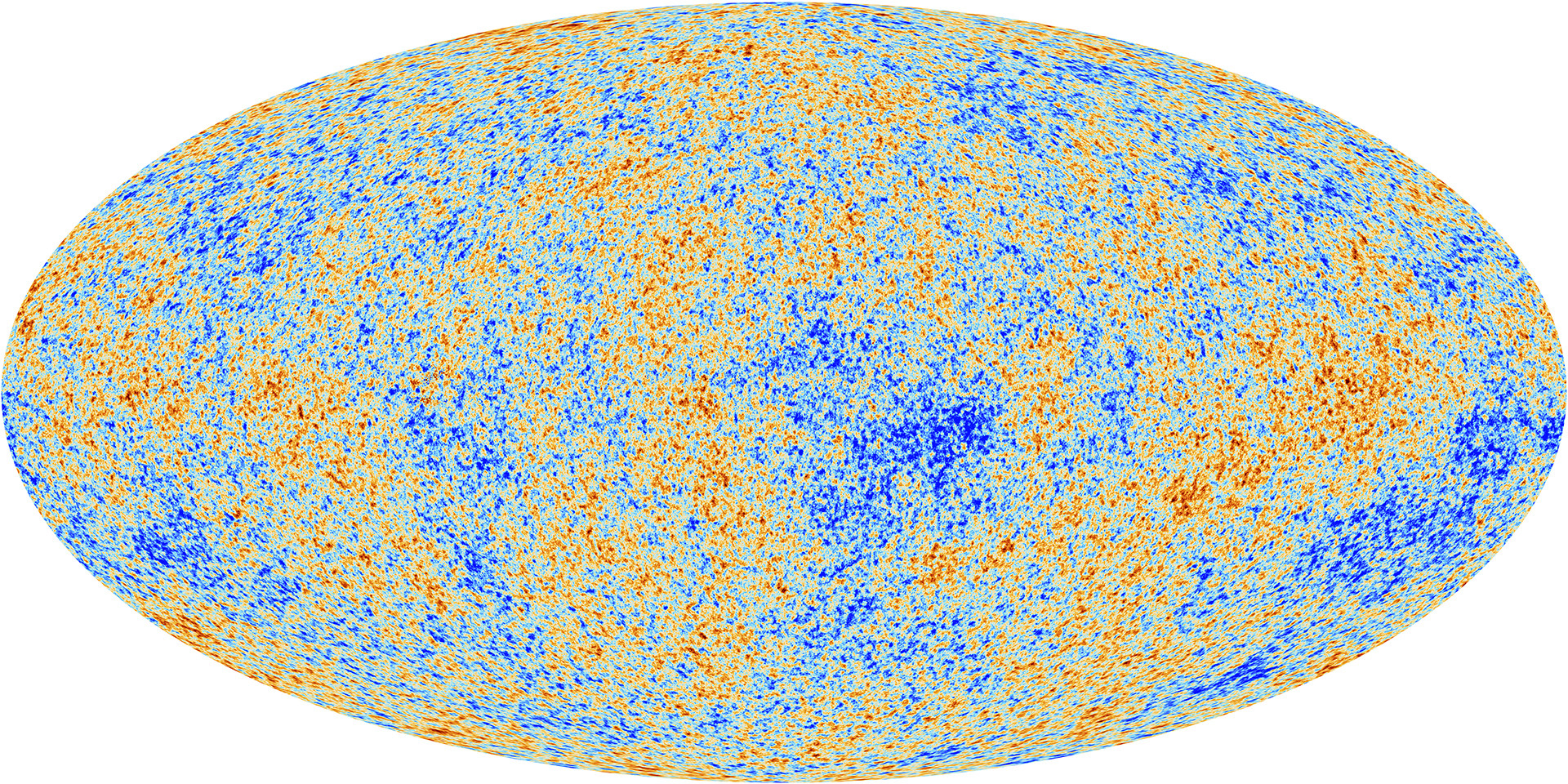
私たちの宇宙がトーラスのように接続されているかどうかはどうすれば分かるのでしょうか？

それは宇宙が平坦でありかつ大きさが有限であることを確かめることができればそれが分かります。

そのカギは宇宙背景放射の中にあります。

初期の宇宙では物質の密度の揺らぎが波として存在していました。

これは音波によく似た性質を持っています。音波も空気の密度の波だからです。

弦をはじいて出る音波の波長（音の高さ）は弦の長さによって決まります。

同じ様に宇宙の物質の密度の揺らぎの波長は宇宙の大きさによって制限されます。

宇宙より大きな波長の揺らぎは存在できません。

この宇宙の密度揺らぎの情報は宇宙背景放射から読み取ることができます。

密度揺らぎの波長に上限があれば、宇宙が有限であるという証拠になります。

研究チームはコンピュータシミュレーションの結果と宇宙背景放射のデータを比較して、宇宙の大きさを求め、その結果を今年2021年7月に発表しています。

研究の結果、宇宙の大きさはなんと観測可能な宇宙の限界（約450億光年）の約3～4倍程度というものだったそうです！

仮に平坦でかつこのように有限の大きさだった場合、宇宙は本当にトーラス型である可能性があります。

ただし今回の研究の結果が正しかったとしても、宇宙の大きさは観測可能な宇宙よりも大きいので、無限に連なる自分の後頭部を見たりすることはできなそうです。

それでももし私たちが巨大な多次元の平坦ドーナツの表面に住んでいると考えると、本当にロマンがありますよね！

今後も宇宙の形にまつわる研究が進んでいき、新発見がもたらされることに期待しましょう。