他校からも続々と見学に来る授業

　すーっと、すがすがしい風が通り抜ける教室。現代アートの美術館のようなモダンな外観でありながら、一歩中に足を踏み入れるとまるで山荘に来たかのようなぬくもりと癒やしを感じる。世界的建築家・隈研吾氏が監修した校舎は、2017年のグッドデザイン賞にも輝いた。

　神奈川県鎌倉市にあるカトリック系の私立中高一貫校・栄光学園中学高等学校を訪れた。2018年の東大合格者数は77人。開成、筑駒、麻布、灘に次ぐ全国第5位の超進学校である。東京大学名誉教授の養老孟司氏、そして前出の隈研吾氏も同校出身だ。

　この学校に、井本陽久さんという数学の教師がいる。40代後半。知る人ぞ知るカリスマ教師だ。ここでは生徒たちからの愛称「イモニイ」で呼ぶこととする。イモニイの授業を見学するのはこの日が初めてではない。自分の記録をたどると、最初の見学はもう5年以上も前のことであった。

　東京の某女子進学校の数学の授業を取材した際、「手法」が井本先生のそれとそっくりだった。聞けば、まさに、イモニイの授業を参考にしたのだという。神奈川の某男子進学校もイモニイの「手法」を真似ている。そして今回の授業には、神奈川県の公立進学校３校からも、数学教師たちが見学に来ていた。

　「最近見学がとても多いですね。アクティブラーニングとか探究学習とかをやりなさいと言われていても、どうやっていいのかわからなくて、参考にしたいと言われます」（イモニイ、以下同）

　理科や社会の授業であれば、アクティブラーニングや探究学習の形式は割と容易に想像できる。しかし数学でどうやって……。そう悩んだ数学教師たちがイモニイの授業を見に来るのである。

　イモニイが担当するのは主に中学生の幾何である。いま、日本の中学校・高校の全体的な傾向として、大学入試で直接的に得点に結びつきやすい代数に時間をかけ、幾何をおろそかにする風潮があるが、開成にしろ灘にしろ、トップ進学校では中学生のうちに幾何を徹底的にやる点が共通している。特に証明問題に時間をかける。決して飛躍を許さない論理的思考力を、中学生のうちに鍛え上げることが、あらゆる学びの土台になるのだ。

　その土台づくりが、栄光学園におけるイモニイの大きな役割だ。そしてその成果のごく一部が、東大合格者数であるといって差し支えないだろう。ちなみにイモニイ自身も、栄光学園の出身で、東大を卒業している。

　イモニイの授業の特徴は３つあると私は思う。

　１つはゲーム性。授業の最後は、各自が課題プリントの問題をどんどん解いていく。１問解き終わるごとに教卓にいるイモニイに見せに行き、「YES！（正解）」か「Ouch!（不正解）」かを判定してもらう。正解すると、生徒はすぐさま自分の席に戻り、次の問題にとりかかる。同時にイモニイは手元のパソコンに何やら入力する。各生徒がいつどの問題をクリアしたのかをすべて記録し、それをポイント換算し、成績に加味するしくみになっている。生徒からしてみれば「ポイントゲット！」というわけだ。授業終了のチャイムまでできるだけ多くのポイントをゲットしようと、生徒たちは目の色を変える。

　２つめは集団性。新しいことを習い、それを使って難しい問題を解くときには、５〜６人のグループでアイディアを出しながら取り組ませる。どこに補助線を引いたらいいか、どんな定理を使えば証明ができるか、本当に論理的に正しいか、お互いに意見を言い合いながら、問題を解く。複数の視点や発想を取り入れることで、生徒たちの理解が促進される。机に突っ伏したまま「わかんねぇ」と時間だけが過ぎていくことも避けられる。

中学生のうちは論理の組み立てに集中

　３つめが、先述の「手法」。これこそがイモニイの幾何の真骨頂。幾何の証明問題の答案には一定の「お作法」が求められる。理屈はわかっていたのに証明の“文章”の書き方に不備があって減点されたという思い出があるひとも多いのではないだろうか。しかしイモニイの授業ではひとまずそこは置いておく。たとえば「下図のときAB//CD（ABとCDは平行）を証明せよ」という問題の正解は、通常ならばこうなる。

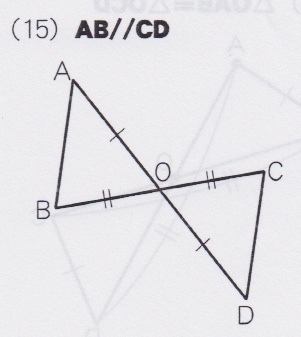
　△OABと△ODCにおいて、問題の条件より、OA=OD、OB=OC

　対頂角は等しいから∠AOB=∠DOC

　二辺とその夾角が等しいから、△OAB≡△ODC

　よって∠OAB=∠ODC

　2直線がほかの1直線と交わってできる錯角が等しいならば、2直線は平行なので、AB//CD　（Q.E.D.（証明終了））

　しかしイモニイの授業では、たった３文字で終わり。

　正解は「（あ）（か）（（う））」（※実際には括弧ではなく丸囲みの文字）。

　どういうことか。

　（あ）（か）（（う））は、それぞれ「公理」を表す。（あ）は「対頂角の大きさは等しい」。（か）は「２つの三角形において二辺夾角相等で合同」。（（う））は、（う）「２直線が平行ならば、他の１直線が交わってできる錯角は等しい」に対してその逆「２直線が他の１直線と交わってできる錯角が等しいならば、２直線は平行である」を意味していて、結果、生徒たちは根拠として使っているのが、（う）なのか（（う））なのか、（A→Bなのか、B→Aなのか）を明確に把握することから逃げられないしくみになっている。

　これらの「公理」を、イモニイの授業の中では「鍵」と呼ぶ。「この問題は、どの鍵とどの鍵をどんな順番で使えば開けられる？」などと使う。授業の初期段階では、「公理」によって「定理」を証明していく。授業の中で証明された「定理」には記号が与えられ、それが新たな「鍵」となる。そうやって証明のための「根拠の鍵束」を増やしていく。

　これらの記号は当然イモニイの授業だけで通用するルール。大学入試ではきちんと「お作法」通りの答案を書かなければ点はもらえない。しかし、イモニイはこういう。

　「本来、論理と答案作成は別物なんです。中学生のうちは答案の文章の完成度を上げることに時間をかけるよりも自分の考えの中で無意識に根拠とされているものや「当たり前」としているものをきちんと意識化する習慣を身に付けることのほうが大切。そうやって破綻のない論理を組み立てる経験を積み、その面白さを知ってほしい。そのためにあえて答案作成は後まわしにしています。もちろん根拠の意識化が身に付いてから、並行してしっかり教えます」

　英語に例えるならば、「三単現のSが抜けていたり、時制の一致が間違っていたりしても、文章の構造が正しくて意味が通じればいいじゃないか。その代わりどんどん作文して発話して、場数を踏もう」というようなものだ。

　「ときどきいるんです。数学的なセンスが抜群で、論理の組み立ては誰よりも速くて正確なのに、答案作成に不備があるために減点されてしまう生徒が。それではせっかく得意なはずの幾何が嫌いになってしまいますよね」

　中には軽度の発達障害をもつ生徒もいる。そういう生徒は得てして答案作成が苦手だったりする。数学に限らず、細かいところで減点され、自信を失うことがある。しかしイモニイの授業で幾何に得意意識をもつと、ほかの教科にも自信をもち、全体的に成績が向上することも多いという。

宿題は出さない。ライバルはスマホやゲーム機

　証明問題の正解は多くの場合１つではない。グループ作業では、生徒同士「これ、（う）（（お））（う）（き）でも解けるけど、（う）（う）（き）だけでも行けるんじゃね？」のような会話が飛び交う。各グループで出てきたさまざまな発想を拾い集め、イモニイが「あそこのグループでさ、こんな解答があったよ。（う）（お）（け）（き）。どう？　これ面白いよね。どうしてこれで解けるのかわかる？」などと解説する。

　先述の東京の女子進学校も神奈川の男子進学校も、この「手法」をまねしているのである。答案作成の「お作法」という難しいことはひとまず抜きにして、生徒たちはパズルゲームを解くような感覚で幾何に取り組むことができるようになる。全国の学校で真似すればいい。イモニイも、このやり方を自分だけの専売特許にしようなどとはこれっぽっちも思っていない。だから、見学を歓迎するし、場合によってはライバルに当たるともいえる他校の教師にも自作の教材を渡してしまう。

　イモニイは宿題を出さない。しかし「やりたいひとはやっていいプリント」を配付する。要するに強制ではない自宅学習用プリントだ。自宅でこれを解いて、イモニイに提出し、正解すれば、そこでも「ポイントゲット！」となる。１学年180人程度だが、コンスタントに130人くらいは提出してくれる。そしてその中に、名解答・珍解答・誤解答があり、次の授業の教材として使わせてもらう。

　イモニイが模範解答を示すことは一切ない。生徒たちは自分たちの正答・誤答で学ぶ。そのため、答えを与えられるのではなく、あくまでも自分たちの力で学びを広げていく姿勢が維持される。

　「僕のライバルはスマホやゲーム機です。彼らが家に帰ってゲームばかりやっていたとすれば、それは僕が渡した問題が、ゲームよりもつまらなかったということです」

　模範解答のプリントを配るときには、同じ証明をした生徒たちの名前を列挙したり、「D組の○○が、このクラスの△△とまったく同じ珍しい証明の仕方に気付いていたよ」などと話してみたり、一人一人の答案にしっかり目を通していることがわかるように生徒たちにフィードバックする。

　場合によってはその日のうちには解説せず、モヤモヤを持ち帰ってもらう。登下校の電車の中や、風呂に入りながら、解法を思いつきそのモヤモヤが晴れたときにはアドレナリンが大放出する。そうやって、幾何の証明問題を提示されると、つい「どの鍵があれば開けられるかな？」と反射的に頭が回転し始めてしまう生徒たちが育つ。

　イモニイの授業は自ずから躍動的になる。誰かが鮮やかな答案を披露すれば「おーーー！」という歓声が沸く。自分が解けなかった問題についてクラスメイトが出した正答をイモニイが紹介してしまえば「あーーー」という納得感と悔しさが入り交じったような声が漏れる。イモニイすら思いつかなかったような珍解答を目にしたときには「これ、ド変態だろ！」という驚愕の叫びが上がる。イモニイがユニークな答案を取り上げて、「これもかなり変態だな」と笑うと、その生徒はガッツポーズする。

　難問に歯が立たなくて、生徒たちがしゅんとしているときには、イモニイはこう言って励ます。

　「3カ月後にはみんなできるようになってるから、大丈夫。だって考えてごらんよ。3カ月前はこんな問題できなかったでしょ。みんなものすごい進歩してるんだから」

　授業の様子を見ていた神奈川県立高校の数学教師たちもその様子を見て目を輝かせる。そのうちの一人は感激を抑えられない様子で私にこう言った。「これが本来の学びなんですよね。学びって本当は楽しいんですよね」。普段の自分たちの授業とのあまりの違いに、ポジティブな意味でのショックを受けたようだ。

　さて、そろそろ今日の授業も終わり。「ポイントゲット！」を狙う生徒たちがイモニイの前に並ぶ。チャイムが鳴ったらおしまいだ。最後の生徒がイモニイに答案を見せたとき、チャイムが鳴る。正解か不正解か、クラス中が注目する。クイズ番組の、みのもんたのように思わせぶりな表情をするイモニイの口から出たのは「YES！」。クラス中が拍手した。

子供たちの「プルッ」とした躍動感が好き

　「これからの社会はこうなるはずだからこんな能力を育てようとか、大学入試改革の方向性を先読みしてこんな授業にしてみようとか、そんなことは私にとってはどうでもいいんです。目の前の子供たちがうんうんうなりながら問題に取り組んで、最終的には『わかった！』と目を輝かせてくれたときのあの『プルッ』とした躍動感が好きなんです。それを見たいがためにやっているようなものです」

　実はイモニイには栄光学園教員とは別の顔がある。栄光学園での授業がない日には、栄光学園以外の生徒を対象にした学習教室を開いている。教えるのは数学だけではない。というより、教科という概念がない。

　栄光学園業務時間外の、限られた時間の中でやっているので、残念ながらいまのところ生徒の一般募集はしておらず、縁あって出会った子供たちだけを相手に、「プルッ」とした躍動感を引き出したくて、やっている。入会に際し、学力は問わない。普通の公立校の生徒もいれば、超進学校の生徒もいる。入会してもらうときには保護者にこう宣言する。

　「学校の成績を上げることを目的にはしません」

　それでもいいと、保護者は子供をイモニイに託す。

　そこでは、どんな授業が行われているのか。明日はその学習教室の様子をレポートする（2018/7/6 12:00すぎに公開予定）。→続きの記事はこちら