2020年ノーベル経済学賞は、スタンフォード大学のポール・ミルグロム教授とロバート・ウィルソン名誉教授が受賞。「オークション理論の改良と新しいオークション形式の発明を評して」が理由。

応用事例としてまっさきにあがるのが、米国FCC（連邦通信委員会）の「電波オークション」「周波数帯オークション」です。これは、携帯端末事業などに使える無線周波数帯の使用免許を競売にかけるというものです。市場規模は何千億～数兆円になると思います。

「新しいオークション形式の発明」というのは、複数の財を同時に売り出す「組み合わせオークション（複数財オークション）」に関するものでしょう。これは、入札者が複数の財を組み合わせて「パッケージ」とすることができて、そのパッケージごとに値段が異なるのが特長です。

組み合わせオークションは、複数の使用免許を同時に競売にかけるのに適しています。全米の無線周波数帯使用免許といっても、全米をカバーする使用免許がひとつだけ競売にかけられているのではありません。全米をいくつかの地域にわけ、それぞれの地域での使用免許が同時に競売に出されます。組み合わせオークションでは、個々の免許を別々に競り落とすのではなく、複数の免許のうち、いくつかを組み合わせてパッケージを作り、そのパッケージに入札することが可能になっています。

Exposure Problem（露出問題）を解決

組み合わせオークションがつかえない場合の問題は、Exposure Problemです。たとえば、テレビ地上波の電波利用権を地域ごとに競売にかけたとき、

　価値（地域Ａ）＝２０００億円

　価値（地域Ｂ）＝２０００億円

という経済価値がある場合でも、

　価値（地域Ａ＋地域Ｂ）＝８０００億円

という価格付けも十分にありえます。これは、当該事業者にとっては地域間に相乗効果が見込める場合です。２地域で同時に放映できれば、それぞれの価値２０００億円×２地域に加え、相乗効果分４０００億円が追加されると考えてみます。

以上のような相乗効果が見込めるケースでは、１地域ごとの利用権をばらばらにオークションにかけることは望ましくありません。なぜなら、相乗効果を見込めたとしても、パッケージで入札できないかぎり、そうした相乗効果分を入札値に反映させにくいからです。この問題が、入札者が片方の財しか入手できず赤字に陥ってしまうリスクにさらされる（exposed）ので、"Exposure Problem"として知られています。例えば、競り上げオークションの途中で、

　競り値（地域Ａ）＝３０００億円

　競り値（地域Ｂ）＝３０００億円

となった場合は、どうすればよいのでしょう。

　両方を競り落とすことができれば、両方合わせた価値８０００億円に対して、支払いは６０００億円なので、競り上げてもよいかもしれません。でも、もし、片方しか競り落とせなかったら、大損です。

　ですから、ＡＢをセットで６５００億円という値付けでもできないかぎり、競り上げオークションはここで止まってしまい、財の配分は非効率的で、オークション収益も最大化されません。こうしたExposure Problemの発生を避けるためには、パッケージオークション、組み合わせオークションが有効なのです。

Threshold Problem（閾値問題）

では、組み合わせさえできれば、問題は解決するのかというとそうではありません。Threshold Problem という、もうひとつの問題があります。例えば；

　事業者Ｘ　価値（地域Ａ）　＝１００億円

　事業者Ｙ　価値（地域Ｂ）　＝１００億円

　事業者Ｚ　価値（地域ＡＢ）＝１３０億円

という経済価値がある場合にそれが起こります。収益を最大化する配分は、事業者Ｘ・Ｙに、それぞれ地域Ａと地域Ｂのライセンスを１００億円で供与することです（収益２００億円）。[追記訂正：market clearing価格をもとにするので、収益１３０億円と捉えるべきでした。]

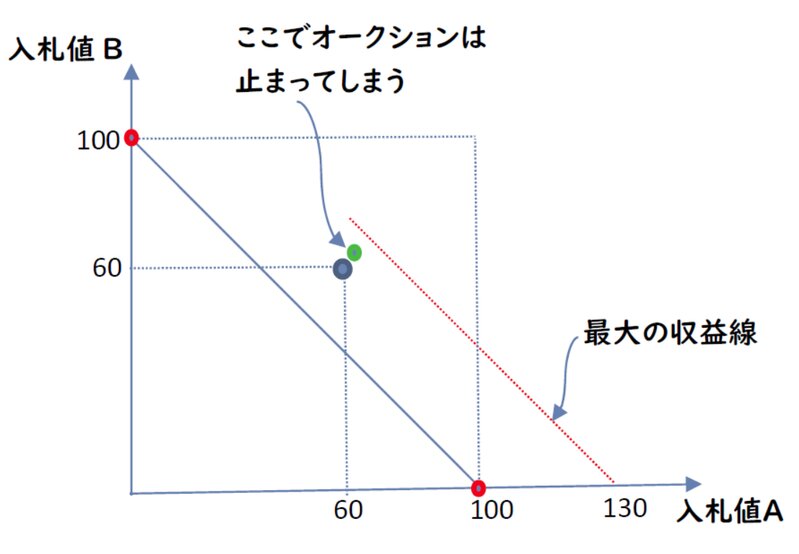
ところが、組み合わせ競り上げオークションの途中で、

　事業者Ｘ 競り値（Ａ）　＝　６０億円

　事業者Ｙ 競り値（Ｂ）　＝　６０億円

　事業者Ｚ 競り値（ＡＢ）＝１２５億円

となったら、何が起こるでしょうか。ここで、事業者ＸとＹの間にタダ乗り問題が発生します。本来ならば、ＸとＹがそれぞれ、６５億円に同時に競り上げれば、事業者Ｚからライセンスを取り戻せます。しかし、入札参加者同士のコミュケーションは禁止されているのもあり、それは不可能です。

すると、ＸかＹかのどちらかが、あと１０億円上乗せしてくれれば、事業者Ｚに勝てるわけです。ここで、ＸとＹはお互いにそれを期待しながら、無駄に時間が経ち、オークションは終了してしまうかもしれません。そうなると、オークション収益は１２９億円で、最大化されず、ライセンスの配分も経済学的に非効率的となってしまいます。

このように、組み合わせオークションをそのまま使えばよいというわけではありません。競り上げオークションには、独特のダイナミズムがあり、そのなかではオークション参加者同士の相互作用や学習が起きます。これを分析するのには、経済学で特に発展したゲーム理論が有効だったという背景があったのです。ミルグロム教授の大きな貢献のひとつがこの分野での大活躍です。