ツイッターアンケートで社会調査、その効果的な方法
少し前の話だが、ツイッターにアンケート機能が導入された。
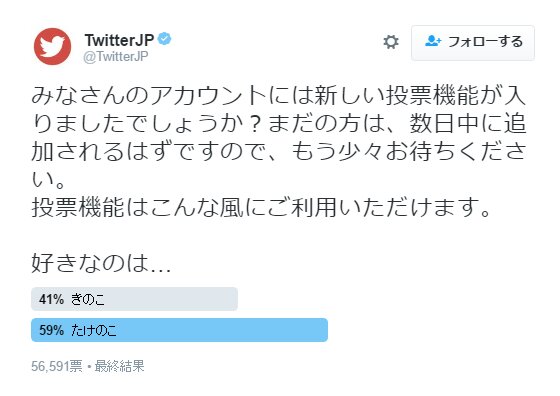
つぎの画像がその例だ。
要は、質問文と選択肢を設定すれば人気投票のように遊べますよということである。この画像のアンケートのように、まあ、他愛がないものが大半である。
この画像のように、最終結果は各選択肢のパーセンテージしか表示されない。ということは、意見の分布くらいしかチェックできないのではと思われがちだ。しかし、色々と工夫すれば「複数の現象間の関係性を調べる」(の真似事)にも使える。
2×2のクロス表
真っ先に思いつくのが2×2のクロス表である。選択肢は4つまで入れられるからだ。
2×2のクロス表とは、二つの水準をもつ変数、たとえば「賛成/反対」とか「経験あり/なし」の関係を見るものである。
もちろん、そのままだとこの分析はできないので、選択肢の作り方に多少の工夫が必要だ。
たとえばつぎのような工夫がいる。(※ちなみに、「問い」自体はくだらないものなので真に受けないで下さい)
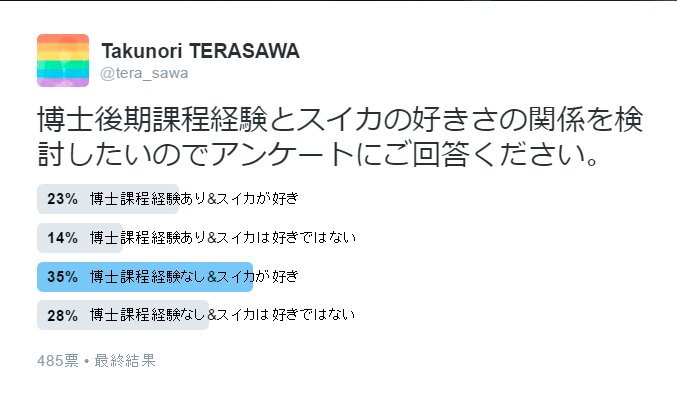
博士後期課程経験とスイカの好きさの関係を検討したいのでアンケートにご回答ください。
博士課程経験あり&スイカが好き
博士課程経験あり&スイカは好きではない
博士課程経験なし&スイカが好き
博士課程経験なし&スイカは好きではない
コツは、このように選択肢に二つの条件を入れ込むことである。スイカでなくてもなんでも行ける。たとえば・・・
- エグザイルが好き & HeySayJUMPが好き
- エグザイルが好き & HeySayJUMPが好きではない
- エグザイルが好きではない & HeySayJUMPが好き
- エグザイルが好きではない & HeySayJUMPが好きではない
- 進研ゼミをやっている & 恋人がいる
- 進研ゼミをやっている & 恋人がいない
- 進研ゼミをやっていない & 恋人がいる
- 進研ゼミをやっていない & 恋人がいない
再集計方法
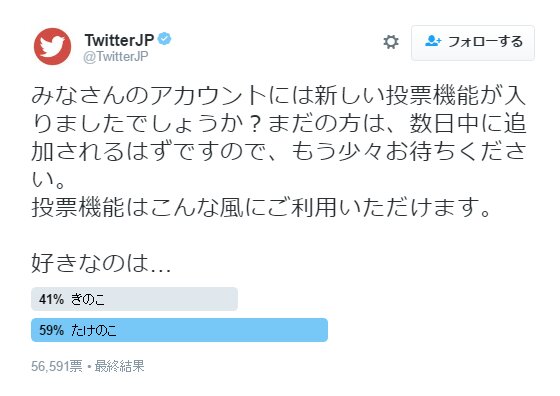
先程の「スイカ好き×博士課程在籍経験」の結果を見てみよう
最終結果には、各選択肢のパーセンテージとトータルの投票数しかない。なので、一手間かけて各票数を算出し直したほうが後で楽だ。
まあ、一手間と言っても、単純に全投票数とパーセンテージをかければいいだけなのだけど。
- 経験あり×好き :485×23% = 111.55
- 経験あり×非・好き:485×14% = 67.9
- 経験なし×好き :485×35% = 169.75
- 経験なし×非・好き:485×28% = 135.8
人数のはずなのに小数点以下を含んだ数字が出てしまっているのは、丸め誤差のせいである。まあ、あまり気にせず、四捨五入してしまってよい(全部足し直すとオリジナルの全投票数と一致しなくなる場合もあるが気にしないのがコツ)
得られた数字を2×2の表の形式にする
| |スイカ好き|好きではない|
|経験有| 112人 | 68人 |
|経験無| 170人 | 136人 |
これだけでも状況はわかるが、つぎの画像のように、行あるいは列ごとにパーセンテージを算出し直すとわかりやすい。

この画像の例だと、列ごと(表のタテ方向を列という)に小計を出して、各人数をその小計で割っている。
結果、博士課程在籍していた人の6割強はスイカ好きだが、そうでない人でも6割弱はスイカ好きがいるので、たしかに多少の差はあるが、たいした差ではないということがわかる。
まあ、関係が見られないのも当然だ。
「博士課程に行くとスイカ好きでなくなる」というのは驚きの結果は当然ながら出なかった。
もし知識があるひとであれば、このデータからさらに統計学的検定も可能である。
画像の下についている情報がそれである。
(ただし、検定までするならば、前述の丸め誤差にはある程度慎重な対処が求められるのでご注意を)。
ツイッターアンケートの利点
最後に、ツイッターを利用したアンケート調査(の真似事)の利点を簡単に書いておきたい。
それは何と言っても手軽さである。
卒論や中高生の自由研究では、ネット経由でアンケートをばらまくことがよくある。たいていはSNSやメーリングリストで回答を呼びかけるのだが、必ずしも回収数は良くない。協力してあげたくても、何度かクリックしてアンケートフォームを開き、かつ質問文を読んで何十個あるかもわからない質問文に回答していくというのはとても億劫に感じてしまう。
一方、ツイッターアンケートは、質問文がツイートに最初から書き込まれているし、クリック1回で回答が終了する。上記のアホみたいな問いのアンケートであっても、500近い票が集まるのである。
この手軽さは、逆に、他人の時間を奪わないという利点でもある。ツイッターユーザを対象にしており、回答のためにわざわざユーザー登録などをしてもらう必要もない。
また、最終結果は(アカウントをクローズドにしない限り)誰でも見ることができる。多くの人にアンケートの協力だけさせて、結果については周知しないというようなものもあるが、そういうことにはならない。
とはいえ、難点は山ほどある。設問の自由度は低いし、複雑な分析には向かない。ただ、単純な問いで、かつ、大至急調べたいことがあるのなら、これを使ってみて損はないはずである。
「2×2クロス表」以上のこと
今回は、2×2のクロス表を扱ったが工夫次第では、もっと複雑なクロス表も扱うことができる。
たとえば、「血液型(A/B/O/AB)」と「血液型性格診断への態度(信じる/信じない)」というのを既にやったことがある。
また、3重のクロス表、つまり「変数X」「変数Y」「変数Z」という3つの変数間の関係を見るものもやったことがある。(次の記事を参照)
これらの作り方についてはまた後日。