宇宙人は存在するか? ねずみが象を超える日 ~数学センスで万事解決(第2回)~

【宇宙人は必ず存在する!】
宇宙人は地球以外にも存在するのでしょうか.人類以外に知的生命体は存在するのかという問題です.自己中心的な人類を踏襲して,それを宇宙人と呼ぶことにしましょう.さすがの自己中心的な人類であっても,自分以外の宇宙人が存在するであろうことは暗に認めています.では存在だけではなく,交流することはできるのでしょうか.この問題への一つの回答がドレイクの方程式と言われるものです(下図).
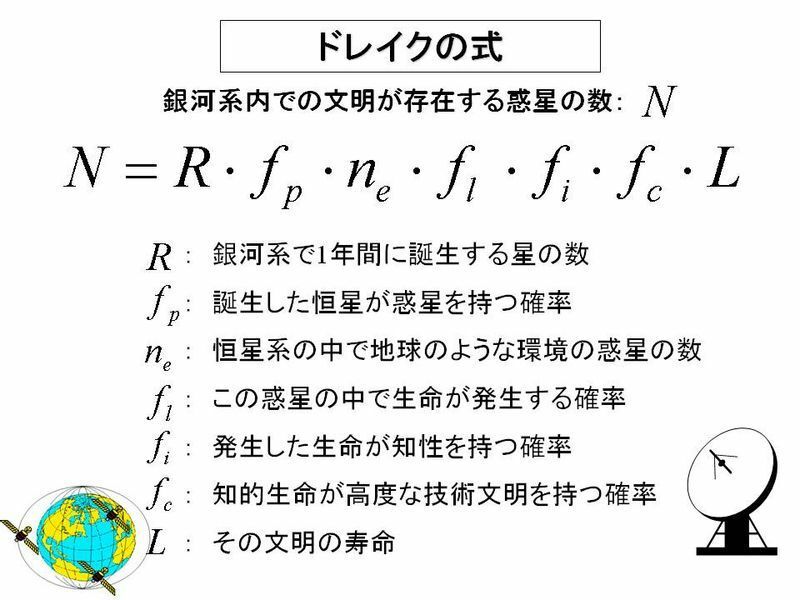
この方程式の解Nは,人類がコンタクトできる可能性のある宇宙人の数を与えています.この式に異論をはさむ人は多くなく,広く認められています.Nが1以上であれば,コンタクトできる可能性が高いということになります.それぞれのパラメータ(変数)の値に異論はあるものの,Nが1以上になる説得力ある回答も数多く見られます.一時期,宇宙人探索で有名になった著名な天文学者であるカール・セーガンはNが1以上になる可能性が高いことを指摘しています.では,人類はすでに宇宙人と交流をもっているのでしょうか.一般には肯定的な意見が強そうには思えません.ドレイクの方程式は認められていますが,その変数に適当な理由をつけて代入するだけで,宇宙人とコンタクトできることになってしまうのです.ちなみに,ドレイクの方程式だけに頼ったわけではありませんが,44年前に打ち上げられ,現在も地球から約227億Km離れた地点を航行しているボイジャー1号には,宇宙人への音声やイラスト等で表されたメッセージが搭載されています.
【ねずみがゾウを超える日】
方程式や数値を与えられると,その信頼性を熟考する以前に,納得させられてしまうことが多々あります.ダレル・ハフ著,高木秀玄訳「統計でウソをつく法」(ブルーバックス,講談社)は,原著では67年以上前に書かれましたが,現在でも十分参考になり,また,この本に書かれた手法でのウソがまかり通っています.昔も今も数字やグラフを与えられれば騙されやすいという傾向があるのです.
数字は信じられない事実を教えてくれる場合もあります.たとえば,「指数」や「対数」に関わる問題です.関数ととともに,中学校の数学でつまずいてしまう「指数・対数」ですが,馴染みがない概念であり,直観的な理解は困難です.その困難性を象徴する問題が約400年前の江戸時代初期に書かれています.和算家の吉田光由による塵劫記という,江戸時代300年以上にわたって読まれ続けたベストセラー数学書での問題です.現代語訳で書くと,
正月にネズミの夫婦が子供を12匹生むとする.翌月の2月には,この親ネズミを含めて,それぞれのつがいのネズミがまた12匹生むとする.するとネズミは総計98匹となる.このように毎月生み続けると年末の12月には総計何匹になるか
という問題です.答えは何匹でしょうか.これが驚くべきことに276億8257万4402匹になるのです.「ねずみ算式に増える」という急激に増えるたとえは,この問題に由来します.この解法は割愛しますが,指数による計算結果なのです.同じような問題で,「米粒
」の問題があります.様々なストーリーに絡めた問題となっていますが,核心の部分だけ抜き取れば以下の通りです.
一か月後に,3俵(1年分の米,約180Kg)もらうのと,今日から米粒1粒,明日は2粒,明後日は4粒というように2倍ずつ一か月にわたってもらうのとどちらが得か.
という問題です.これは2倍づつ一か月,もらう方が得なのです.最初の1週間では総計127粒しかもらえません.これは大さじのスプーン一杯で約2g,一口のごはんにしかなりません.しかし,30日後には,約10億粒にもなり,20トン,つまり3俵どころ
か,300俵以上,100年分以上の米になるのです.
では,さらに身近な問題を与えましょう.新聞紙を手元に用意してください.それを2つにきれいに折りましょう.そしてそれをさらに2つに折ります.さらに2つ,と次々に折っていきます.10回も折ると,現実には折ることができなくなってしまいますが,ずっ
と折り続けることができたとして,45回折るとどれぐらいの厚さになるでしょうか.答えはこの記事の最後に.
【誕生日の問題】
「ねずみ算」は感覚的には理解し辛い数の増え方でした.人の感覚と数の実際の問題には大きなズレがある場合が少なくないのです.以前,超能力を扱ったテレビ番組を見る機会があり、会場にいた数百人の中から何人かを選んで、同じ誕生日の人を見つけるという能
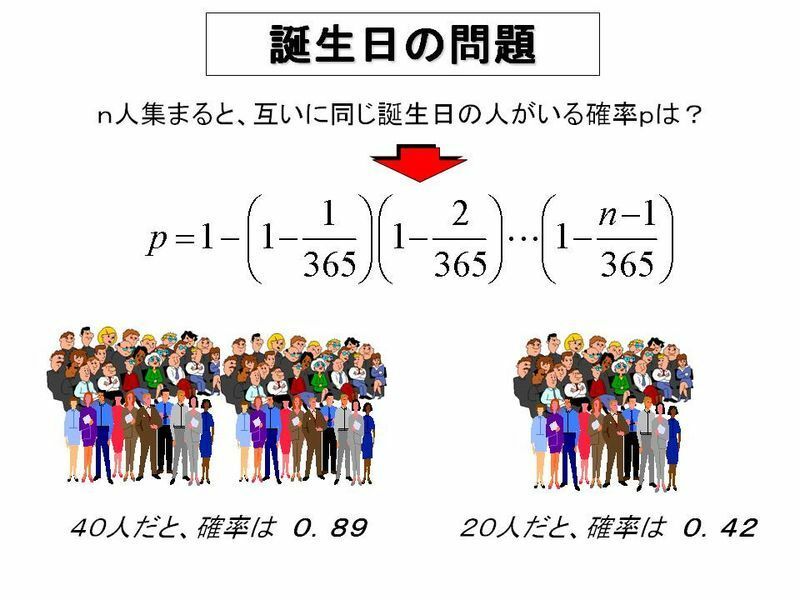
力を披露していました。もちろん、その能力を持つと言われる人は来場者の誕生日を知りません。その人が20人ほどを選ぶと、誕生日を同じ日に持つ人がいるというのです。テレビを見ていると、目隠しをしたその超能力者と言われる人が、客席を指差して、20人ほどを指し示しました。選び終わった後、その20 人ほどが一人一人、誕生日を言うと、確かに同じ誕生日の人が一組いるのでした。拍手と共に番組が終ったわけですが、これは誰にでも真似の出来るトリックがあるのです。もちろん、あらかじめ誕生日を知っているというような単純なトリックではなく、人の数の感覚のズレを利用したトリックなのです。実は誰がやっても同じことが出来るのです。つまり、誰が、どの20人を選んでも同じ誕生日を持つ人が選ばれる確率が、通常の感覚で思われているよりも高いのです。この問題は「誕生日の問題」と言って、「確率」という数学の分野では、よく取り上げられる問題です。詳細は省きますが、20人集めれば、その中で互いに同じ誕生日を持つ人が少なくとも一組存在する確率は、0.42程度になり、コインの表裏を当てるのと同じ程度の確率で成功するのです。ですから、誰でもが、数回、同じように20人を選べばほぼ成功することになるのです(下図).
【新聞紙折りの解答】新聞紙1枚が0.03mmとすると,驚くことに約100万Kmにもなります.地球と月の距離約38万Kmよりも離れてしまうのです.










