なんと、次は「91年後」…2025と45の、じつに意外な関係…次回までに「素数の年は何回ある」でしょうか
奇数と平方数の面白い関係
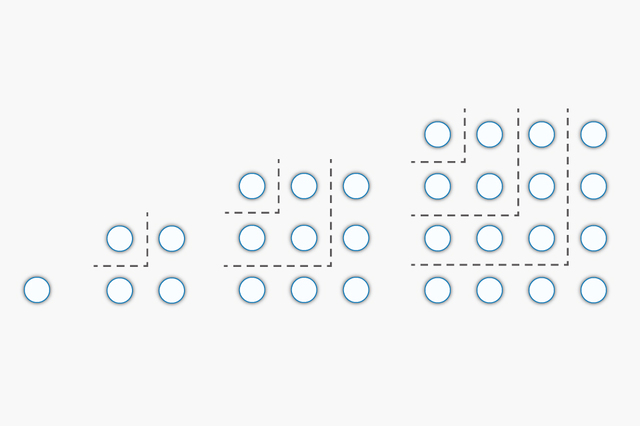
2025年を表す上記の数式の意味を考えてみましょう。数の世界の面白さを味わっていただけたらと思います。 まず、 1+3+5+7+…+89=45² です。この式は、「奇数の和が平方数である」ことを表しています。 89までの和がたまたま平方数になるのではなく、どの奇数までの和も平方数になります。 1=1² 1+3=4=2² 1+3+5=9=3² 1+3+5+7=16=4² … となり、奇数を足していくと、すべて平方数になります。奇数と平方数の面白い関係です。 一般に、 1+3+5+…+(2n-1)=n² が成り立ちます。この関係は、次の図を見れば視覚的にも明らかです。
立方数と平方数のふしぎな関係
次に、 1³+2³+3³+4³+5³+6³+7³+8³+9³=45² です。自然数の3乗を「立方数」といいます。この式は、「立方数の和が平方数になっている」ことを示す式です。これも、9³までの和がたまたま平方数になっているのではなく、どの立方数までの和も平方数になります。 1³=1=1² 1³+2³=9=3² 1³+2³+3³=36=6² 1³+2³+3³+4³=100=10² … となります。 証明はしませんが、一般に 1³+2³+3³+…+n³=(1+2+3+…+n)² という興味深い関係が成り立ちます。 それでは、最後の式はどうでしょうか?
平方数についての深い法則
4つめの式は、 2025=45²=9²+18²+18²+36² です。 この式の背後には、平方数についての深い法則が関係しています。上の式がどのように導けるかを説明すると、 45²=9²・5²=9²(1²+2²)²=9²(1²+2²+2²+2⁴)=9²+18²+18²+36² のようになります。いちばんの中心になるところは、 5=1²+2² と、素数5が2つの平方数の和で表せることです。そこで2つの平方数の和について考えてみましょう。