循環節を図示してみると……？

循環節の図示。0から9の数字を振った円周に、循環節に出てくる数を順に結ぶ

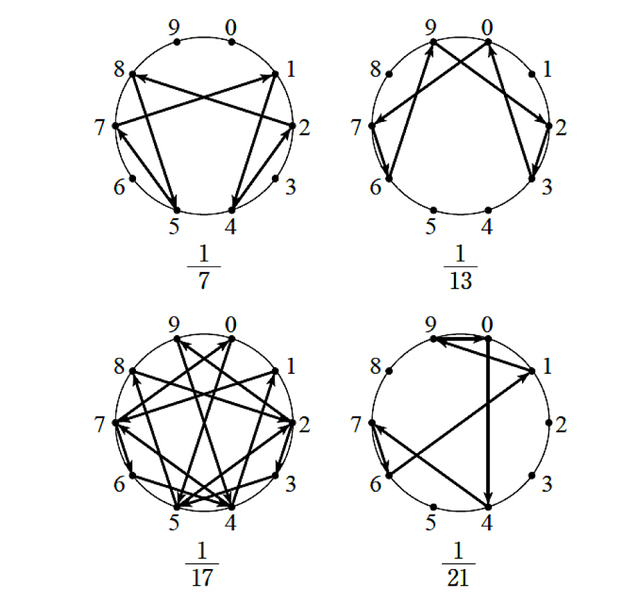
循環節から図形を作ってみよう。『中学数学で磨く数学センス』でも繰り返し指摘しているように,「数を図形でとらえる」(あるいは「図形を数でとらえる」)ことは「数学する力」を身につけるための近道であり,すなわち数学センスを磨くことに直結している。 円周を10等分し,0から9の数字を振る。循環節に出てくる数を順に結ぶと,何が現れるだろうか。 1/7の循環節:1, 4, 2, 8, 5, 7 1/13の循環節:0, 7, 6, 9, 2, 3 1/17の循環節:0, 5, 8, 8 2, 3, 5, 2, 9, 4, 1, 1, 7, 6, 4, 7 1/21の循環節:0, 4, 7, 6, 1, 9 これらを図示すると,次の図(図「循環節の図示」)のようになる。 8, 8や1, 1と同じ数が続くところは図示していないが,その数字自身を結ぶ小さな円を描いてもよい。 これらの図形は,1/21を除くと線対称な図形になっている。なぜだろうか。 分母が素数で循環節の長さが偶数のとき,循環節を前半と後半に分けて足すと,9が並ぶ数になることが知られており,「ミディ(Midy)の定理」とよばれている。 たとえば, 1/7の循環節では142+857=999, 1/13の循環節では076+923=999, 1/17の循環節では05882352+94117647=99999999である。2/7の循環節でも285+714=999, 5/13の循環節でも384+615=999 である。 この事実が,循環節の長さが偶数のときに,それを図示したものがどれも線対称の図形になることを示している。 *数学センスを磨くポイント* 数の列を図として表現すると,対称性を見つけられることがある。 さて,分数を小数表示したときに,1/3=0.333…のようにずっと続くのではなく,1/4=0.25のようにあるところで止まる小数を「有限小数」ということを,冒頭でご説明した。 この有限小数で表される分数(たとえば,　1/2,　1/4,　3/4,　1/5…など)から,面白い性質が見えてくるが,ここで重要な役割を果たすのが,中学校で学ぶ「素因数分解」だ。このような性質に気づけるようになると,あなたの「数学センス」もかなり“レベル”が上がるに違いない。 *次回は、4月3日公開予定です。 中学数学で磨く数学センス　数と図形に強くなる新しい勉強法 中学3年間で学ぶ重要ポイントを抽出し、教科書では習わない視点でとらえなおす「新しい時代の新しい勉強法」──。「数を図形でとらえ」「図形を数でとらえる」=「数学する力」が誰でも身につく！〈理系に強い子ども〉に育てたい親世代へのヒントも満載！