『るろうに剣心』左之助の「二重の極み」を実践できるポイントはこれだ!
こんにちは、空想科学研究所の柳田理科雄です。マンガやアニメ、特撮番組などを、空想科学の視点から、楽しく考察しています。さて、今日の研究レポートは……。
かっこいい必殺技が、理屈をきちんと説明されてると、自分でもやってみたくなりますね。たとえば『るろうに剣心』相楽左之助の「二重の極み」とか!
この技、パッと見では、ただのパンチのようだが、破壊力がすさまじい。大木や巨大な岩も、まるで砂のように粉砕する!
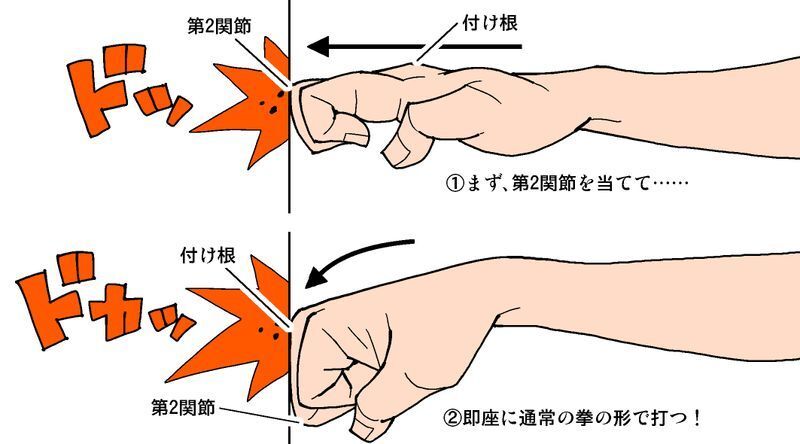
そのヒミツは、独特の打撃法にある。まず拳の第2関節で打撃し、即座に第1関節を曲げて通常の拳の形で打つ。
つまり、拳の2つの関節で、連続して打撃を与える、というものだ。
この技を教えてくれたのは、破戒僧の悠久山安慈。左之助も、最初はソフトボール大の石をいくつかの破片に割るくらいしかできなかったが、「一週間でこの技を極める」と言い放ち、不眠不休で稽古を続ける。
そして7日目の朝、ついに石を粉々に砕いたのだった。
『るろ剣』の人気はいまも衰えず、「北海道編」もが描かれているので、今日もどこかに「二重の極み」をやろうとしている人がいるに違いない。
そこで、この技について考察し、どうすれば実践できるかをお伝えしたいと思いますぞ~。
◆「抵抗」とは何だろうか?
――などと大口を叩いてしまったものの、これは難題だ。
そもそも、途中で第二関節を当てようと当てまいと、拳が持っている総エネルギーは変わらないはずである。だとすると「二重の極み」は「拳のエネルギーを2回に分けて打つだけの技」ということに……?
待て待て。結論を急がず、この技を創始した安慈の言葉に耳を傾けよう。彼が左之助に説明した内容を要約すると、こうなる。
すべてのものには抵抗が存在するため、拳打の衝撃は物体に伝わり切れない。
だが、第一撃の衝撃が抵抗とぶつかった瞬間、第二撃を入れれば、衝撃は抵抗を受けることなく完全に伝わり、石を粉砕する。
うむむ、わかったような、わからないような説明だ。
とくに「すべてのものには抵抗が存在するため、拳打の衝撃は物体に伝わり切れない」という一文がきわめて悩ましい。
科学で「抵抗」というと、物体の運動を邪魔する力のこと。たとえば、平らな床でボールを転がすと、摩擦や空気抵抗に邪魔されて、そのうち止まる。このような力が「抵抗」であり、衝撃の伝わり方には関係ない。
そこで筆者なりにアレコレ考えてみたのだが、安慈はひょっとして「物体の破壊を邪魔するもの」の意味で「抵抗」と言っているのではなかろうか。
だとすれば、それは科学の言葉では「弾力性」ということになる。
岩石にも弾力性はある。たとえば、一辺10cmの立方体の花こう岩に、1tの荷重をかけると0.01mm縮み、荷重を解除すれば元に戻る。この弾力性が衝撃を吸収するため、少々の衝撃では壊れない。しかし、180tの力を加えると、弾力性の限界を超えて破壊される。
そこで、「抵抗」を「弾力性」に読み替えると、安慈の言葉はこうなる。
拳打の衝撃は石の弾力性に吸収されるが、第1の衝撃で弾力性の限界近くまで変形させた瞬間、第2の衝撃を与えれば、石は粉砕される。
おおっ、充分ナットクできるようになったと思いませんか!?
◆ヒジョ~に科学的なワザだ!
この解釈が正しければ、「二重の極み」を受けた石の内部では、次のような現象が起こっていることになる。
第1の衝撃は、石の内部を伝わり、反対側で反射して返ってくる。そこへ第2の衝撃を与えると、それも内部を伝わり、やがて第1の衝撃と出合う。2つの衝撃が出合った瞬間、石は大きく変形し、ついには破壊に至る……!
その威力を、具体的に考えてみよう。
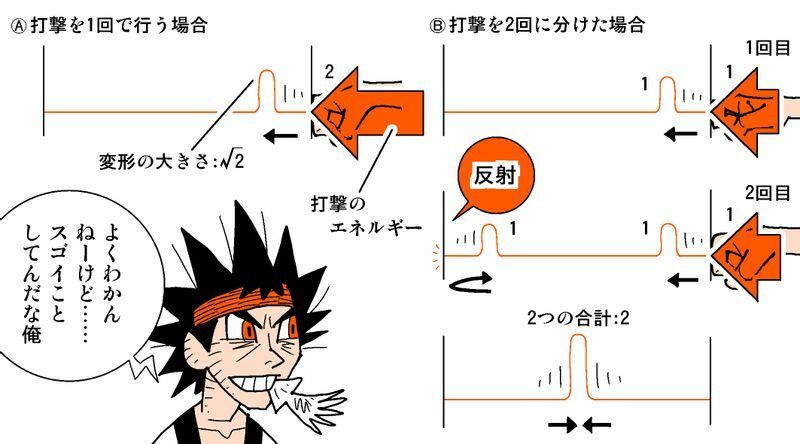
「二重の極み」で打ち込まれる2回の打撃のエネルギーを、それぞれ1としよう。それによる石の変形の大きさも1とする。
まず、打撃2回分のエネルギーを1発のパンチに集中させるとどうなるか? 衝撃のエネルギーは2となり、これは「変形の大きさ×変形の大きさ」に比例するから、変型の大きさは√2≒1.4になる。
では「二重の極み」なら?
2つの衝撃が出合うとき、変形の大きさはシンプルな足し算になる。第1打による変形は1、第2打による変形も1。当然1+1=2である。
つまり、同じエネルギーでも、衝撃を2回に分けたほうが、石は大きく変形して壊れやすいということだ。
「二重の極み」には、科学的な意味が充分にあった!
◆「二重の極み」のやり方は?
筆者独自の解釈とはいえ、原理的にはすっかり腑に落ちて、ワタクシはいまモーレツに感動しています。あとは、これを実践するための具体的な方法を考えるだけだ!
石に与えた衝撃はたちまち衰えるから、第1撃を打ったら、すぐさま第2撃を打ち込みたい。
最大の効果を期待するなら、第1波が石の反対側に着いた瞬間、第2波を送るのがよい。こうすれば、2つの衝撃は石の中央で出合うことになる。
ここでは、左之助が修行に使った石の厚さを10cmと仮定して考えよう。
衝撃が岩石を伝わる速度は、秒速4千m。第1波が反対側へ達するまで0.000025秒だ。この間に、第1関節と第2関節のあいだの分だけ拳を動かせばよいわけである。
筆者が、自分の手のその部位を測ると6.5cmだった。0.000025秒間に6.5cm動くパンチの速度は、秒速2600m=マッハ7.6。
――というわけで、具体的な方法がわかりました。
「二重の極み」を実践しようと思ったら、マッハ7.6でパンチを繰り出して、連続的に2つの関節で打撃を与えればよい!
左之助の体重は71kgだから、彼がマッハ7.6のパンチを放つと、そのエネルギーはライフル弾の8千発分。直径4.5m、重量140tの岩を砕けます。スバラシや!
と喜んだものの、うーん、マッハ7.6か。
わずか一週間でそこまでに達した左之助は、恐るべき人物だったのだなあ。
いやいや、遠い目になっている場合ではない。あなたも私も「二重の極み」を実践したかったら、左之助を見習って、さあ修行だ修行!