こんにちは、空想科学研究所の柳田理科雄です。マンガやアニメ、特撮番組などを、空想科学の視点から、楽しく考察しています。さて、今回の研究レポートは……。

『トリコ』は、2008年から足掛け9年にわたって「週刊少年ジャンプ」に連載されたグルメ×バトルの驚異的なマンガであった。

物語の舞台は「地球」だが、いまわれわれが暮らしている地球ではなく、謎のエネルギーを吸って膨張した「地球」。

この星で、人間が生活圏にできているのは「人間界」だけだ。

そのまわりには、未知の生物がウヨウヨひしめく「グルメ界」が広がっている……という設定だった。

そんなすごい話だけに、魅力的なキャラがたくさん登場したが、ここでは「猿王バンビーナ」の行為について考えたい。

猿王バンビーナが「巨大な山」を海に向かってぶん投げると、山は海面で何度もハネ返りながら、はるか彼方に消えていく。

現実の世界に、水面に小石を投げる「水切り」という遊びがあるが、猿王は、それを小石ではなく「山」でやったのだ。

そして一週間後、海の反対側から、小石が海面を跳ねながら帰ってくる！

そう！　投げられた山は、地球をグルリと一周し、途中で削れてどんどん小さくなり、小石となって戻ってきた、ということだ。

あまりにもスケールが大きい！

いかにも『トリコ』らしいエピソードだが、どうすればこんなコトが実践できるのだろうか？

◆山が地球を一周！

猿王バンビーナは、グルメ界に君臨する八王（8匹の強大モンスター）の一角を占める、サルの怪物である。

このエピソードが登場するのは、『トリコ』のコミックス第34巻だ。

猿王が海辺の岩に座っていると、遠くから小石が海面を跳ねながら近づいてくる。

それを見つけた猿王は、石の飛んでくるほうへ駆け寄って、額で石をコンと受けて「キャッキャッ」と喜ぶのだった。

――これぞグルメ界名物「水切り山」。

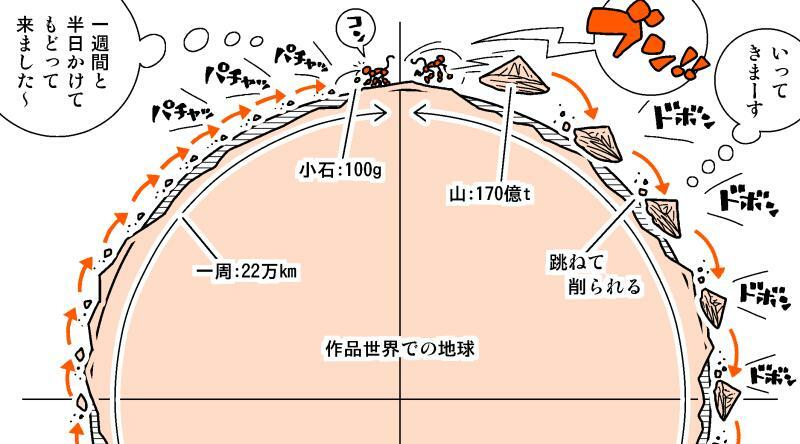
作中の説明を要約すれば「高さ1500ｍの山がマッハ1で海を跳ね、スピードを落とすことなく１週間かけて周囲22万kmの地球を一周し、風や陸地や海に削られて小石になる」。

高さ1500ｍの山を、マッハ1で投擲して、周囲22万kmの地球（現実の地球は周囲4万km）を一周！

あまりにもすごい行為だが、どんな力があればこれができるのか？

まずは、猿王が投げた山の大きさと重さを求めよう。

マンガで計ると、山の直径は高さの2.6倍。

富士山のようにきれいな円錐形だ（富士山の直径は高さの11倍だから、この山はとても尖っている）。

高さが1500ｍだから、すると直径は3.9km。

そして、富士山と同じ玄武岩でできていた場合、重さは170億ｔだ。

猿王は、こんなモノをマッハ1で投げたのだ。

猿王バンビーナは、主人公のトリコ（身長２ｍ20cm・体重230kg）より、少し小柄だった。

その体格でモノを投げるとき、動かす腕の距離は1ｍほどだろう。

たった1ｍで、重量170億ｔのモノにマッハ1のスピードを与えたとしたら、猿王の出した力は99兆ｔだ！

……数字がすごすぎて、書いてる筆者も何がどうすごいのか、わかりません。

実感するために「もしトリコが猿王に同じ力で投げられたら？」を計算してみると、なんとマッハ27万で飛んでいく。

地球の重力も太陽の重量も振り切って、銀河の果てに消えることになる。

◆「頭にコン」の奇跡！

すごいすごいと感心してばかりだが、科学的に興味深いポイントがもう一つある。

それは、猿王に投げられた重さ170億ｔの山が22万kmを跳ねるうちにどんどん削られていって、最後は小石になって猿王の額にコンと当たったこと。

この「コン」が重要だ。

自然界の岩も、川の上流から下流にゴロゴロ運ばれているうちに、割れたり削られたりして小石になるから、22万kmも跳ねるうちに山が小石になるのは、理屈のうえでは納得できる。まことに科学的だ。

そしてマンガの描写を見ると、額に当たった小石は100ｇほどの大きさだった。

170億ｔからこのサイズになったとすると、170兆分の1に削られたわけである。

筆者が驚くのはここだ。

一周して帰ってきたとき、コンと額に当ててもいい大きさになっているのが、もうモーレツに奇跡的！

周囲22万kmをマッハ1で一回りするには、正確には1週間と12時間かかる。

すると、山は「1日ごと」に80分の1になったはずなのだ。

「1分あたり」に直すと、0.3％ずつ小さくなっていった計算になる。

この「1分あたり0.3％減」という減少率は、気温や投げる速度によって、変動するはずだ。

減少率がわずかに違っても、結果は大きく変わってしまう。

たとえば、1分あたり0.4％ずつ削られるとしたら、22万kmを一周して戻ってきたときの重さは、3mgにまで小さくなる。

3mgとは蚊の体重くらいで、その重さの石とは直径1.3mmほど。

砂粒みたいな大きさだから、戻ってきても猿王は気づかないかもしれないし、額に当たっても「コン」という音はしないだろう。

逆に、1分あたり0.2％ずつしか削られなかったら、戻ってきたときの重さは7.3ｔ。

デカい。これだけ重いと、やっぱり「コン」では済まなくて、巨大な岩が額に「ドッカーン」！

あらためてマンガをよく見ると、猿王の足元には同じくらいの大きさの小石がたくさん転がっている。

これすべて、戻ってきた水切り山なのだろう。

つまり猿王は、その日の気温などの気象条件を全地球的に把握し、それに合わせて山を投げる速度を調節していた……。

猿王バンビーナは、パワーだけでなく、知能もモノスゴイということだ。

『トリコ』では、こういう魅惑のエピソードがいっぱい描かれて、本当に楽しいマンガであった。

また続きを描いてもらいたい。