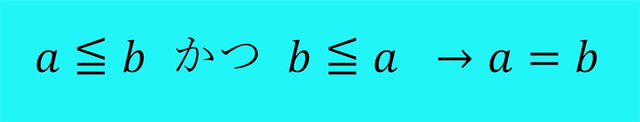「イチ、ニ、サン…」人類はいつから「数」をかぞえていたのか。「かぞえる」から「自然数」へ、さらに「無限」までかぞえた数学者の考え方
「無限集合同士の濃度」とは
最後に、2つの数aとbの間にa≦bとb≦aが成り立つならば、a=bであることは誰もがよく知っている。 実は、それと同じことが無限集合同士の濃度でも「ベルンシュタインの定理」によっていえる。それゆえ、この定理は集合論では極めて重要であるが、この定理の証明は初学者にとって難解である。 拙著『離散数学入門』では思い切って、具体的な集合の場合にこの定理を証明し、その後でこの定理の一般的な証明を述べた。それによって証明はかなり理解し易くなったようで、難解な証明を理解し易くするための一つの手法であると考える。中学数学の「2次方程式の解の公式」の証明に例えると、最初は具体的な方程式を「解の公式」の証明の流れに沿った形で解いて、次に、「解の公式」の一般的な証明を述べるようなことである。
芳沢 光雄(数学・数学教育)