「ゲーデル数」を使って考えてみると

ゲーデルの考えた符号化(コード化)・再掲「ゲーデル数」

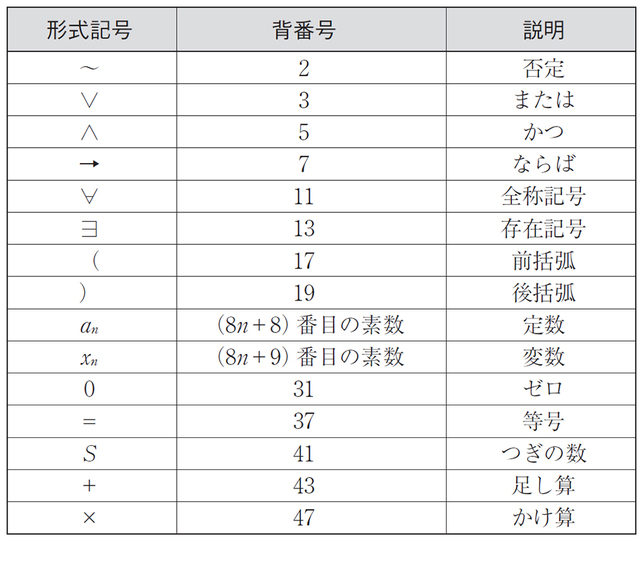
ここで、(8n+8)番目の素数というのはなんだろう。8番目の素数は23、16番目の素数は67、……という具合になっている。なんだか、「0」に対応する31や「×」に対応する47と重複しそうな気がするが、無論、「)」に対応する19の次の素数である23から始まって、47までの素数は飛ばすために8nがかかっているわけだ。ゲーデル数は、このように随所に工夫のあとがみられる。 で、このような基本的な記号がいくつか並んで記号列になった場合は、素数のべきの掛け算であらわす。 たとえば、3つの記号が並んでいて、それぞれのゲーデル数が、l、m、nだとすると、2のl乗×3のm乗×5のn乗が、その記号列のゲーデル数になる。 感覚をつかむために、ちょっと練習してみよう。次の記号列をゲーデル数に変換してください。ここで、以前の記事で紹介した記述法を使います。「次の数字」という概念を、英語の「successor」(次にくるもの、跡継ぎ)の頭文字をとって「S」であらわす。 たとえば数字の1はゼロの次なので「S0」だし、3はゼロの次の次の次だから「SSS0」である。これを使うと、有限の記号により、無限に多い自然数を記述することが可能になる。必ず「次がある」という自然数の性質を凝縮した、見事な記号だ。 練習:3+5=8 「3」はゼロの次の次の次の数だから「SSS0」と書ける。同様に「5」はSSSSS0 、「8」はSSSSSSSS0である。つまり、この記号列は、 SSS0+SSSSS0=SSSSSSSS0 なのである。全部で記号が21個あるから、21番目までの素数が必要になる。「S」に対応するゲーデル数が41、「0」に対応するゲーデル数が31、「+」に対応するゲーデル数が43、「=」に対応するゲーデル数が37なので、最終的に答えは、 241×341×541×731×1143×1341×1741×1941×2341×2941×3131×3737×4141×4341×4741×5341×5941×6141×6741×7141×7331 となる。ぜいぜいぜい。