gettyimages

理系の「3ワカラン」と呼ばれる「ゲーデルの不完全性定理」。「正しいからといって、それが証明可能であるとは限らない」とは、どういうことなのか？　この度、リニューアル刊行されたロングセラー『不完全性定理とはなにか　完全版』のなかから「不完全性定理」、そして異なる視点からゲーデルと同じ証明にたどり着いた「チューリングの計算停止問題」のエッセンスを紹介します。この記事では、「証明できないことは、証明できるのか？」という問いから、天才・ゲーデルの考えた「ゲーデル数」についてみていきます。 【図版】「ゲーデル数」はなぜ必要か？そには「超数学」の視点が必要だった！ *本記事は『不完全性定理とはなにか　完全版』(ブルーバックス)を再編集したものです。

証明できないことは、証明できるのか？

gettyimages

そもそも証明というのは、「公理」に「推論規則」を適用していく作業である。たしかにいろいろな定理を証明することが可能だが、「この命題は証明できません」という定理なんて、いったいどうやって証明すればいいのか。 いちばんの問題は「この命題」という部分である。 「この命題」を具体的に書くと「この命題は証明できません」となる。だから、「この命題」の部分に「この命題は証明できません」を代入してみると(ここでよーく考えてみてください) 「『この命題は証明できません』は証明できません」であり、 「『{この命題は証明できません}は証明できません』は証明できません」 などとなって、永遠に終わらない！　これは、江戸川乱歩の『鏡地獄』みたいなもの。内面が鏡になっている球の中に入ったら、光が無限に反射して、同じ像が無限に見えて、精神がおかしくなっても不思議ではない。物理的には、どこかで光が減衰して、反射は終わるのだろうが、数学ではそうもいかない。 こういうのを「自己言及」(self-reference)という。自分について語りつつ、無限後退を避ける方法はないものか。

天才・ゲーデルの発想「ゲーデル数」とは！

ゲーデルの考えた符号化(コード化)「ゲーデル数」

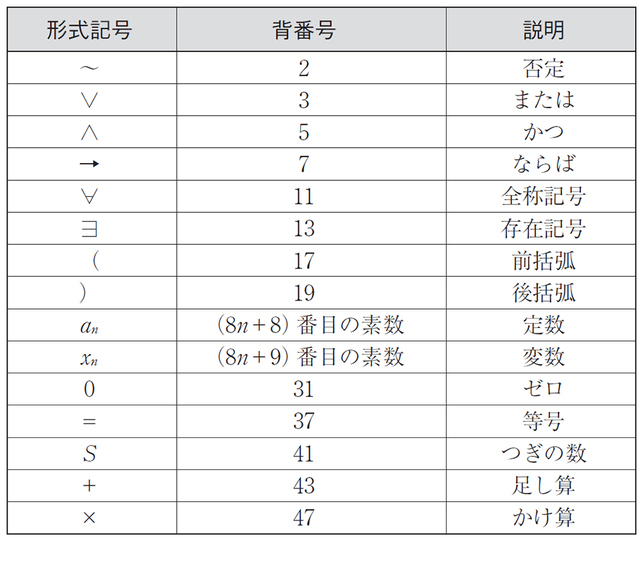
ここでゲーデルの天才は、とんでもないことを思いついた。数学は、数字を扱うものですよね。だったら「この命題」に数字の背番号をつけて、その背番号で呼べばいいのではあるまいか。うーん、なんという数学者らしい解決法。まさに数学者の鏡、じゃなくて鑑ですな。 背番号といったが、専門用語は「符号化」(coding)もしくは「コード化」である。暗号のことを英語では「コード」というが、ようするに、同じ機能をもった別の記号におきかえようというのである。 具体的には、次の表みたいに、まずは基本的な記号に背番号をつける。 ゲーデル数は教科書によってちがいがあるが、大事なことは、形式記号と数字(背番号)の間の変換が1対1でおこなわれる、ということである。ここでは私が学生時代に愛読した『ゲーデルの世界』(廣瀬健、横田一正著、海鳴社)(121ページ)から引用した(ただし、~とSと×は本書の表記に合わせた)。