図を用いた発想で、算数から確率・統計、そして経済学の数学までを見渡してみると【なぜ図を描くのか?】
(エ)各種の統計的なデータを整理して何らかの傾向をつかむ。
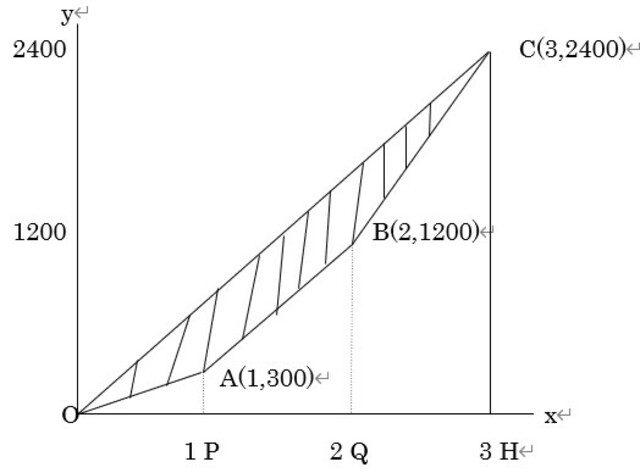
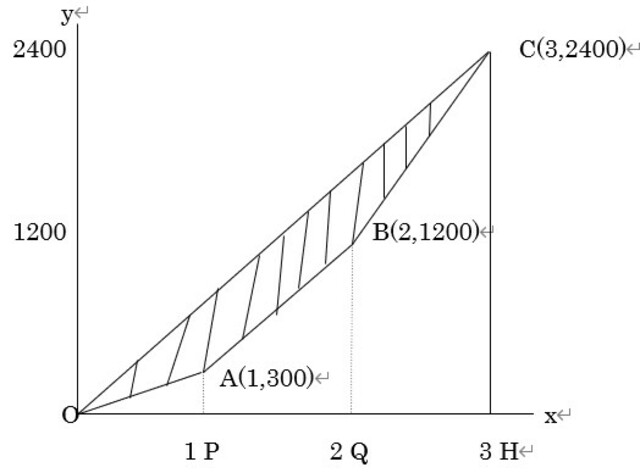
格差を巡る議論は、年々高まってきている。そこで、格差問題を論じるときによく用いられるジニ係数について、例を用いて説明しよう。 いま、国民が3人で構成されている2カ国<1>、<2>想定し、それぞれの国民の年収は低い方から並べて以下の通りとする(単位は万円)。 <1>300、900、1200。 <2>200、200、2000。 <2>国は、<1>国より格差が大きい国であると思うだろう。ただ、どちらの国民の平均年収も800(万円)である。 ここから、ジニ係数を算出するために必要なグラフを準備する。<1>国に関して、年収の低い方から1人分の合計年収は300(万円)で、年収の低い方から2人分の合計年収は 300+900=1200(万円) で、年収の低い方から3人分の合計年収は 300+900+1200=2400(万円) である。いまxy座標平面において、x座標では人数、y座標では上記人数分の合計年収をとるとする。したがって<1>国では、次の3点をとることになる。 A(1, 300)、B(2, 1200)、C(3, 2400)。 さらに原点(0,0)をO、点(3, 0)をHとし、線分OC、CH、および折れ線O-A-B-Cを描き込むと下図のグラフになる。 折れ線O-A-B-Cは1905年にアメリカの経済学者マックス・ローレンツが発表したものであり、ローレンツ曲線と呼ばれている。
経済学の格差指標「ジニ係数」とは
ジニ係数gは、ローレンツ曲線を参考にしてイタリアの統計学者コラッド・ジニによって1936年に発表された指標で、線分OCとローレンツ曲線O-A-B-Cで囲まれた斜線の部分の面積を、三角形OCHの面積で割ったものである。 いま、点(1, 0)、点(2, 0)をそれぞれP、Qとおけば、三角形OCH、三角形OAP、台形BAPQ、台形CBQHの面積は簡単に求まる。 そして、<1>国のジニ係数gは0.25であることが分かる。同様にして、<2>国のジニ係数gは0.5であることが分かる。 <1>国の0.25から、<2>国の0.5へ大きくなることは、対応する斜線部分の面積が大きくなることであり、それは格差が大きくなることを意味している。 ちなみに、上では3つのデータによるジニ係数の説明であったが、一般的な場合の説明も同じである。このジニ係数の発想は、会社内の給与格差や学校内の成績格差の分析など、様々な応用ができることを指摘しておきたい。
芳沢 光雄(数学・数学教育)