図を用いた発想で、算数から確率・統計、そして経済学の数学までを見渡してみると【なぜ図を描くのか?】
(イ) 実際の図形の検討したい部分を扱い易い大きさに表現する。
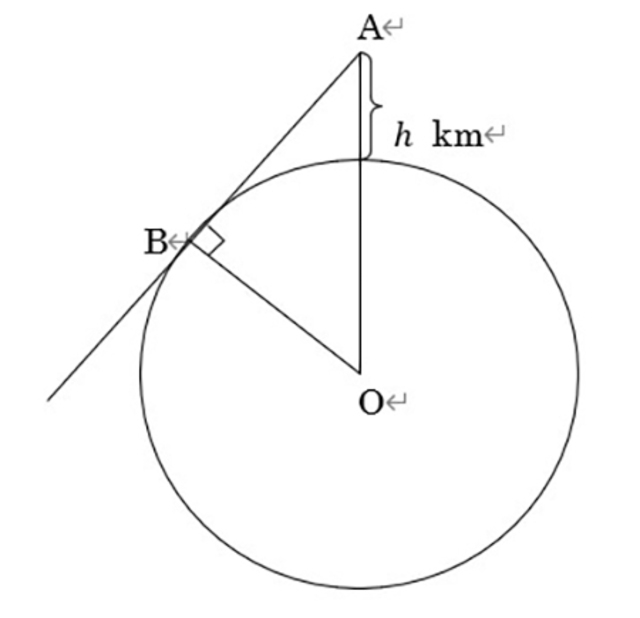
上の図3において、Aは地上hkmの地点、BはAから見渡せる最も遠い地上の点、Oは地球の中心、円Oは三角形ABOを含む平面にある円である。 地球はおよそ半径6400kmの球体をしている。そこでhが分かっていれば、三平方の定理より、 ABの距離×ABの距離+BOの距離×BOの距離=AOの距離×AOの距離 が成り立つので、ABの距離すなわちAからの視界が分かるのである。 東京都の立川市、八王子市、東村山市、板橋区などには「富士見町」という町名があるが、空気の澄んだ晴天の日にそれらの町で遠望が効く場所に立つと、本当に富士山が見えることも説明できるのである。 中学や高校では、頂点に注目して2次関数のグラフを学び、さらに指数関数、対数関数、三角関数などの様々な関数のグラフを、微分を用いて極値も決定して学ぶ。ここで留意しなくてはならないことは、哲学者・数学者であったデカルト(1596-1650)が著書『方法序説』の中で、座標平面の考え方を最初に紹介したことである。関数を座標平面上で視覚的に捉えることの礎にはデカルトの発見があったのである。 なお、教科書や参考書では関数のグラフは、頂点や極値の周辺ばかりに注目している感がある。かつて某大学の入試数学問題に、大域的な視点からのグラフを描かせる問題が出題されたことがあるが、芳しくない成績であった。 y=2のx乗のグラフを大域的な視点から描くと、xが負の部分ではほぼx軸と同じで、xが正の部分ではほぼy軸と同じになる。この視点は、どこかで学んでおきたいものである。
(ウ) 良いアイデアを生み出すためのヒントを模索する
鶴亀算、植木算、仕事算、旅人算などの算数の文章問題は、誰もが小学校のときに学んだことだろう。それらの解法を一々述べることはしないが、解法に向けた良い図を描くことが要点になる。黒板に板書した先生の図を見て、「どうして、あのような分かり易い図を描けるのだろうか」と何度も不思議に思った懐かしい思い出がよみがえる。 環境問題でよく取り上げられるダイオキシン(類)は、ジ・ベンゾ・パラ・ジ・オキシンの構造式の周りにある水素Hが塩素Clに1つ以上置き換わったものである。もちろん、置き換わったものの数が同じでも構造が異なる化合物はいろいろ考えられる。そこで、ダイオキシン(類)は全部でいくつあるだろうか。 この問題の答えは75で、ジ・ベンゾ・パラ・ジ・オキシンの構造式をよく見ながら対称性を考えて1つずつ数える数学の問題になる(拙著『離散数学入門』参照)。