あみだくじの仕組みとは？

図4

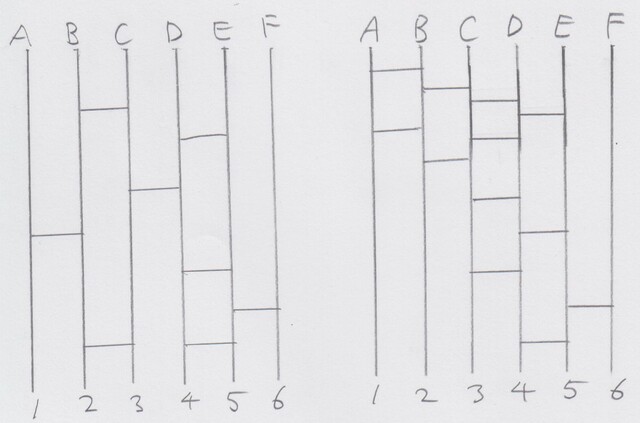
さて、筆者は小学校、中学校、高校での出前授業を今までに200校ぐらいで行ってきたが、多くの生徒に喜んでもらったベスト3は、「誕生日当てクイズ」「膨大なじゃんけんデータからの有利な方法」「あみだくじの仕組み方」である。 「あみだくじの仕組み方」は、上段にたとえばA、B、C、D、E、Fの6人がいて、下段に1等、2等、3等、4等、5等、6等があるとき、誰がどこに辿り着かせたいかリクエストをもらって、速やかにその通りに仕組んで生徒皆に喜んでもらうことである。もちろん上記の拙著にも誰でもできるように説明してあるが、実は数学として極めて大切なことを続けて述べている。 それは、大学で線形代数学を学ぶ人は行列式の導入部分で必ず「偶置換・奇置換の一意性」というものを学ぶ。この性質はあみだくじのある性質と同値(同じこと)なのである。具体例で説明しよう。 左のあみだくじも右のあみだくじも、どちらもAは3、Bは6、Cは1、Dは5、Eは2、Fは4に辿り着く。しかし書き入れた横線の本数は、左は8本で、右は12本である。このように、辿り着く先が全部一致するあみだくじ同士は、横線の本数は異なることはあっても、その本数が偶数か奇数かは一意的に定まるのである。 大多数の線形代数学のテキストでは、古くから「差積」という多項式を用いて「偶置換・奇置換の一意性」を証明している。これは「対称性」を用いた証明ともいえる。他にも、「帰納法」を用いた証明もある(W.I.Millar、1971年)。 筆者は今から20年ほど前に、あみだくじの図を眺めているとき、ふと「2通りに数える方法」で上述のあみだくじの性質、それゆえ「偶置換・奇置換の一意性」の証明を思い付いたのである。それは日本数学会誌「数学」58巻に掲載していただいたが、普通の方々には分かり難い面があった。そこで『離散数学入門』において、誰でも分かるようにその証明を丁寧に述べた次第である。