組み合わせCの考え方

モリ 順列の考え方がわかってきましたね。Cという言葉も出てきたところで、組み合わせについて学んでみましょうか。 アユム Cですね。 モリ では、簡単な問題を用意しました。A、B、C、D、Eさんの5人から2人を選びます。最初に選んだ人にガムを、次の人にチョコを渡します。何通りの選び方ができますか？ アユム えーと、ガムがもらえる候補が5人で、チョコがもらえる候補は...ガムをもらった人を除くので4人。だから、選び方は5×4=20通り！ これは、先ほどのPの考え方ですよね？ モリ その通りです。では今度は、この5人から、アメを渡す2人を選んでください。 アユム 2人選んでどちらにもアメを渡すなら...順番は関係なくなりますよね？ モリ すばらしい着眼点です。そうなんです。A-Bさんを選ぶのと、B-Aさんを選ぶのは同じ意味になります。このように、選ぶ順番を区別しない選び方の通りを「組み合わせ」といいます。 アユム これがウルトラC。 モリ

図

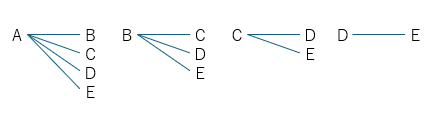
そうです。Combination（コンビネーション）ですね。順列で求めた数から、A-B、B-Aのような同じ要素による並び順の違いを除外する必要があります。 考え方が難しいので、まずは組み合わせの考え方を樹形図で確認しましょう。 組み合わせは下のようになります。

アユム 10通りが答えですね！これも計算できるんですか？ モリ 2人の並び順は 2! (=2×1=2)通りあるので、順列の総数を2!で割ることで組み合わせの数が得られます。 アユム なんか難しいですね。2の「びっくり」はなんですか？ モリ これは階乗（かいじょう）といって、その数から1までのすべての整数をかけていくんです。たとえば、2!=2×1ですね。これで割るので、組み合わせの計算式は次のようになります。 nPr/r!=5P2/2! アユム うーん、ややこしい。ところで、ウルトラCはどこに行っちゃったんですか？ モリ 組み合わせの公式には「C」を使いますnPr/r!=nCr という関係があって、n個の中からr個を選ぶときに使う公式です。 アユム 計算方法はどうなるんですか？ モリ 分子はnから大きい順に数字をr個かけ合わせ、分母はrから1までの数字をかけ合わせます。 アユム 言葉が脳に刺さりません！ モリ では具体的に。5人から2人の組み合わせを選ぶ5C2は、5×4/2×1です。つまり分子はnから大きい順にr個のかけ算、分母はrから1までの数字のかけ算... アユム あ！ 確かに、nPr/r! の形になっている！ びっくりが出てきたときは、全然わからなかったのですが、Cの公式だと思うとちょっと気分が楽になります。 モリ まあ、Cを公式として覚えてしまってもいいでしょう。ただ、公式を暗記する前に、理屈を理解しておくと、さらに覚えやすくなりますよ。