順列Pの考え方

アユム なぜ、かけるんですか？ モリ

図

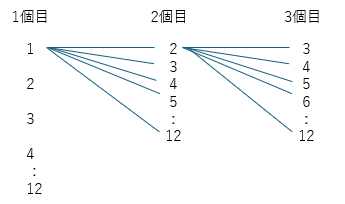
絵をかくとわかりやすいので、かいてみましょう。 状況をシンプルにまとめるとこのような樹形図になります。

アユム 樹形図って、木みたいだからですか？ モリ そうです。ではなぜ、かけ算になるかを見てみましょう。説明のために、鍵には【1】～【12】の番号をつけます。図と照らし合わせて、考えていきましょう。 アユム まずは、1つ目の鍵穴にセットする鍵を選ぶんですね。 モリ そうです。12通りありますね。ここでは、鍵【1】をセットしましょう。 アユム 残りの鍵は、【2】～【12】までの11個です。 モリ では、2つ目の鍵穴に、鍵【2】をセットしましょう。 アユム 残った鍵は、【3】～【12】番の10個です。 モリ ここからが重要です。鍵を【1】と【2】と選んでいるとき、3つ目の鍵穴にセットする鍵の選び方は、何通りありますか？ アユム 残った鍵の個数、10通りですね。 モリ そうです。さらに、【1】‐【3】と選んだ場合は？ 【1】‐【4】と選んだ場合は？ アユム それぞれ、3つ目の鍵の選び方は10通りですね。そうか、10通りの選び方が、2つ目の鍵穴の11通り分だけあるから、2番目と3番目の鍵穴については、11×10通りですね！ モリ その通りです！ こうして、かけ算になります。そして、1つ目の鍵の選び方が12通りあるので…。 アユム 【1】‐【 】‐【 】、【2】‐【 】‐【 】...、【12】‐【 】‐【 】のそれぞれに、11×10通りの鍵の選び方が続くから12×11×10=1320になるんですね！ モリ はい。このように「連続で起きていること」「順番があるもの」を「順列」といいます。 アユム 公式はありますか？ モリ 分子はnから大きい順に数字をr個かけ合わせます。公式では nPr と書きます。 異なるn個のものから異なるr個のものを順列で取り出すという意味です。（Pは、英語の “permutation” （パーミュテーション）から来ています） アユム むむっ。それ…PとかCとか、うっすら記憶はあるけど、めっちゃ苦手でした… モリ ここで、少し得意になりましょう。先輩の場合は、12個の鍵から番号の付いた鍵穴にそれぞれ正しい3つの鍵を選ぶので、12P3＝12×11×10＝1320になります。 そういえば、キャビネットに何が入っているのですか？ アユム お菓子らしいです。お客様から珍しいお菓子をいただいて、大切にとっておいたら賞味期限が迫っているらしく、どうしても開けたいと先輩が言ってました。