【図形問題】正方形の4辺に反時計回りに矢印を描きます。向かい合う辺を矢印の向きをそろえて貼り合わせるとできる図形は?
できることろから、やってみよう!
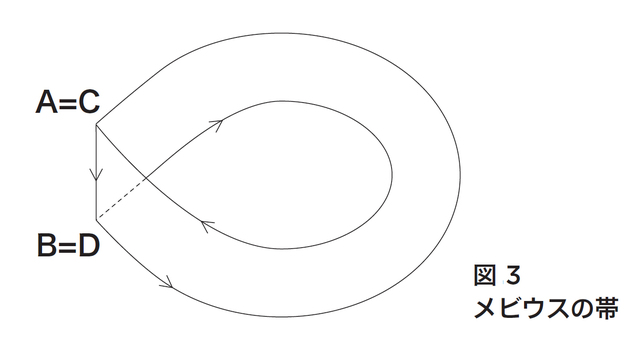
点Aと点Bが重なり合います。点Cと点Dが重なり合います。もしも、この工作が可能なら結果として、4点A、B、C、Dは重なり合って1点になります。 できそうなところから、やってみましょう。まず、辺ABと辺DCを矢印の決める向きが合うように貼ります。これは、メビウスの帯になります(図3)。 辺DAの矢印と辺BCの矢印は図のようになります。向きに注意してください。そのあと辺DAの矢印とBCの矢印を同じ向きに合わせられるでしょうか? なんだか、無理そうな気がしますか。 逆に、さきに辺DAの矢印と辺BCの矢印を同じ向きに合わせ、次に、辺ABと辺DCを矢印の向きが同じになるように貼り合わせても無理そうです。 では、両方の貼り方を同時に行ったらできるでしょうか? これも無理そうです。 以前の記事では「クラインの壺を作る操作」を紹介しました。「クラインの壺」は3次元空R3(*アールスリー:Rは二重線、3は肩付き)の中ではできないのでした。 じつは、この工作も3次元空間R3の中ではできないことが知られています。
この図形は、4次元空間R4の中ならできる!
しかし、もしかしたら4次元空間R4(*アールフォー:Rは二重線、4は肩付き)の中ではできるのでは? と思った方もいるかもしれません。その勘はあたりです! この工作は4次元空間R4の中ではできるのです。4次元空間R4の中に、なんらかの図形ができます。この図形には「2次元実射影空間RP2(アールピーツー)」(*Rは二重線、Pはイタリック体、2は肩付き)という名前があります。 以降の記事では、この「2次元実射影空間RP2」がどんな形をしているのか! ウェルナー・ボーイという数学者が発見した図形を紹介します!
小笠 英志(数学者)