東大も震撼した「円周率が3なんて、けしからん」…「計算力の低下問題」をはるかに超える問題「円が正六角形でいいんですか?」
最も簡単な多角形「正三角形」で考える
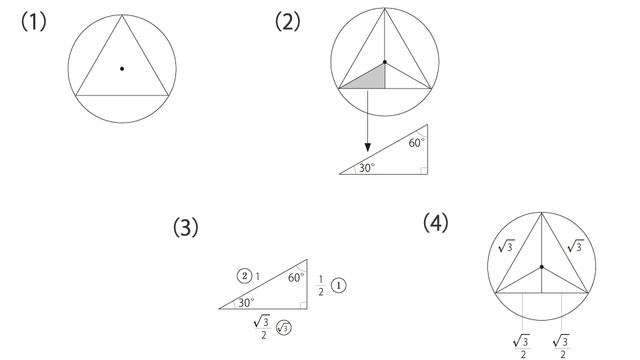
半径1の円に、最も簡単な正多角形である正三角形を収めたのが図(1)で、次の図(2)でアミをかけた直角三角形を取り出します。 この直角三角形の3辺の長さはそれぞれいくつですか? 内角が30°、60°、90°の直角三角形の3辺の長さの比は、1:2:√3 です。今回の直角三角形は、斜辺が円の半径なので、その長さは1で、他の2辺の長さは、図(3)のようになります。 よって、もとの正三角形の周の長さは、図(4)から3√3とわかります。 円周>正三角形の周の長さなので、2>3√3です。この不等式の両辺を2(> 0)で割っても、不等号の向きは変わらないので、 >(3√3)/2 √3 = 1.732…> 1.7なので、 >(3√3)/2>3/2・1.7 = 2.55 これで、円周率が2.55より大きいことがわかりました。 しかし、これでは「円周率が3より大きい」と結論づけることはできません。そこで、3より大きくなるまで、正三角形から正方形、正五角形、正六角形……と順に収め、円に近づけていきます! いったい、何角形になったら、「円周率が3より大きい」ことを証明することができるでしょうか。続いて、正三角形より円に近い正五角形を収めてみましょう。
正五角形で考えてみる
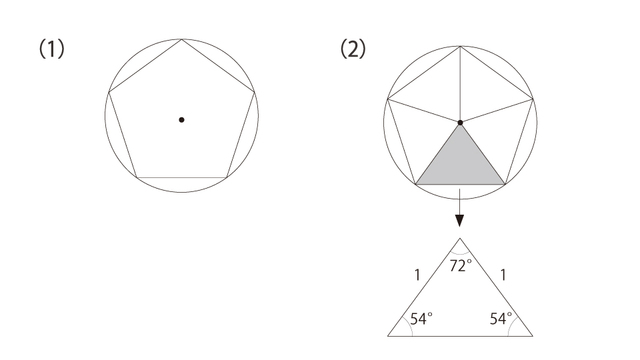
半径1の円に正五角形を収めたのが図(1)です。次いで、図(2)でアミをかけた三角形を取り出します。 円の半径が1なので、円の中心を挟む2辺の長さは1だとすぐにわかります。しかし、この三角形の残る1辺の長さは、(中学数学の教科書の範囲では)求めることができません。
正六角形では?
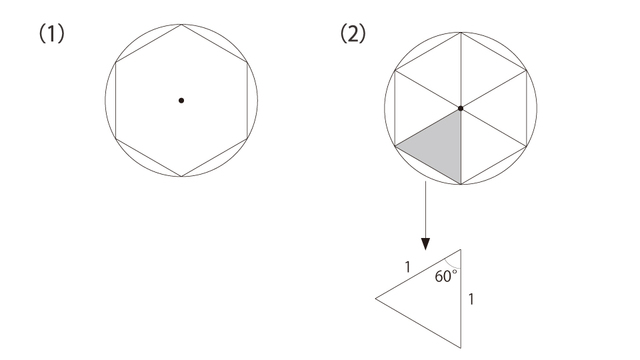
仕方がないので、図(1)のように正六角形を収めます。 図(2)でアミをかけた三角形は、頂角が60°の二等辺三角形なので、正三角形だとわかります。 ということは、残る1辺の長さも1です。よって、円周>正六角形の周の長さなので、 2>6 > 3 これで、「円周率が3より大きい」ことを証明することができました!
【関連記事】
- 【続き】中学数学なら「知っているはず」だけど、改めて問われると即答できない「1≦1は正しいですか」…大学入試で問われる「知識の質」
- 東大、京大の「出題意図」から見えてきた真実「じつは、大学は“知識”は問うていない」…「中学数学の大学入試問題」をわざわざ出題するわけ
- 【関連「先の記事」はこちら】あの「東大の入試問題」は、日本社会に叩きつけた「問題提起」だったのかもしれない…良問にひそむ「数学教育界を揺るがす」衝撃のメッセージ
- なんと「人類史上2番目」に読まれてきた…多くの人が知っている「史上最高の数学バイブル」が示す、じつにシンプルな数学の「神髄」
- 簡単そうなのに、意外に答えられない「正三角形は、二等辺三角形ですか?」…正解より知識の「しんか」が問われます