グラフ理論入門「各人の知り合いの合計は？」

A、B、C、D、Eがいて、AはBの1人だけと知り合いで、BはA、C、Dの3人だけと知り合いで、CはBとDの2人だけと知り合いで、DはB、C、Eの3人だけと知り合いで、EはDの1人だけと知り合い。

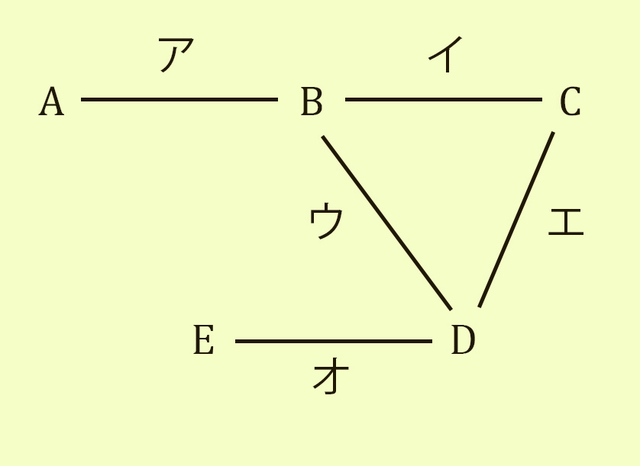
次は、離散数学にあるグラフ理論という分野の一丁目一番地にある定理と本質的に同じ話題の紹介である(拙著『離散数学入門』参照)。 <性質> 人間の集団があって、そこでは任意の2人について、「互いに相手と知り合いである」か「互いに相手を知らない」のどちらかが成り立っているとする。このとき、各人が知っている人数の全員ぶんの合計は偶数になる。 この性質を具体例を使って説明しよう。 ここに5人A、B、C、D、Eがいて、AはBの1人だけと知り合いで、BはA、C、Dの3人だけと知り合いで、CはBとDの2人だけと知り合いで、DはB、C、Eの3人だけと知り合いで、EはDの1人だけと知り合いとする。このとき、互いに知り合いの関係の2人を線で結ぶと、下図を得る。 上図で線の本数は5本である。そして、アはAからの1本とBからの1本を意味している。イはBからの1本とCからの1本を意味している。ウはBからの1本とDからの1本を意味している。エはCからの1本とDからの1本を意味している。オはDからの1本とEからの1本を意味している。 ここで各人が知っている人数の全員ぶんの合計を考えると、 Aからの1人+Bからの3人+Cからの2人+Dからの3人+Eからの1人=10人 となる。 この計算で、アに関してはAからの1とBからの1をカウントしている。イに関してはBからの1とCからの1をカウントしている。ウに関してはBからの1とDからの1をカウントしている。エに関してはCからの1とDからの1をカウントしている。オに関してはDからの1とEからの1をカウントしている。 要するに、アから2、イから2、ウから2、エから2、オから2の合計 2+2+2+2+2=10 をカウントしている。 いま上で具体例を使って説明したことは、最初に述べた「性質」について、「各人が知っている人数の全員ぶんの合計は偶数になる」ことの説明にもなっているのである。そこで、たとえば次の話には嘘があることが分かる。