じつは「2歩進んで1歩戻る」が解決への近道

「実験」と「帰納と演繹」の関係

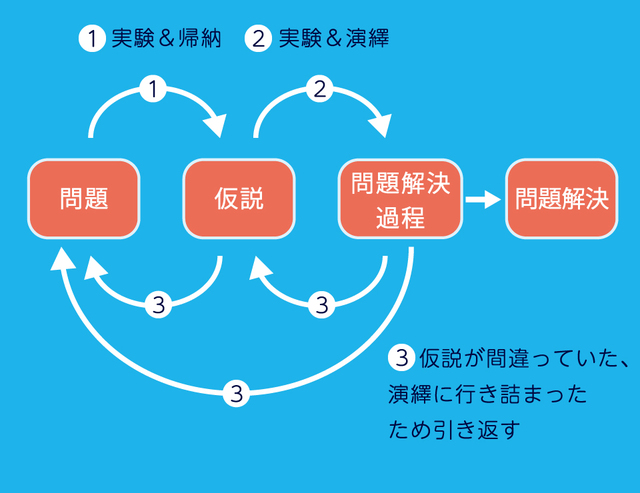
先の記事で紹介した「帰納」でも扱いましたが、今回の例のように、いくつかの「特殊」な場合で正しいことは、「一般」的に正しいことを保証するものではありません。「実験」と「帰納と演繹」の関係をまとめると、次のようなイメージになります。 実験を前提とした帰納(仮説推論)により、仮説を立てることが多く、ときには、演繹の途中でつまずいたときに、実験でアイデアを得ながら、演繹を進めることもあります。そして、仮説が間違っていた、演繹に行き詰まったため引き返すこともあります。「帰納」の結論(「仮説推論」の仮説)は、正しいとは限らないので、この「2歩進んで1歩戻る」等のプロセスも重要です。 「戻る」ことは、決して失敗ではありません。一度は進んだ経験から、次の1歩を踏み出すのが前回よりも容易になるからです。 もちろん、新たなアイデアが出ず、手詰まりになることもあるでしょう。しかし、「この方向に進むと行き止まりだ」という反省的な言語化により、他の方向への歩みが促されることで、必ず解決に近づきます。 大学入試問題は1問あたり20~30分が標準ですから、頭を抱えて考え込むのではなく、どんどん手を動かして「実験」し、「特殊→一般」へと進んでいきましょう。 「百聞は一見に如かず」ならぬ、「百聞は一“験”に如かず」なのです。 中学数学で解く大学入試問題 数学的思考力が驚くほど身につく画期的学習法 有名大学の問題が「解ける喜び」「考える楽しさ」を体感しよう！　中学数学の知識・技術で大学入試問題にトライして、数学の真髄に触れる。