Yahoo!ニュース

「覚えているだけ」では、ざんねんでしかない…「中学数学で大学入試を解く」のに「本当に必要」な知識レベル

配信

現代ビジネス

深い理解が解法を導く「応用」レベル

「4. 総合」のレベル

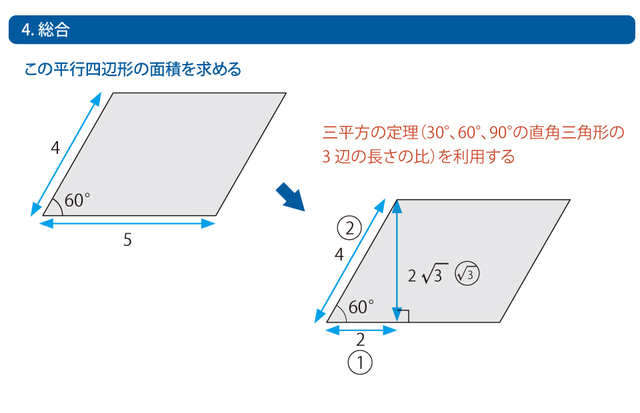
次の図の左上の平行四辺形の面積を求めることができるのが、「4. 総合」のレベルです。 平行四辺形の面積公式(底辺×高さ=面積)のうち、高さがわからないため、右下の図のように三平方の定理(30°、60°、90°の直角三角形の3辺の長さの比)を利用することを考えます。 これで高さが2 √3とわかるので、面積は5・2 √3=10 √3と求めることができます。 平行四辺形の面積公式を深く理解していることによって、三平方の定理を利用する解法にたどり着いたことがおわかりになるかと思います。このように、「問題文中にはないが、必要な公式を引き出すことができる」レベルが「4. 総合」です。 また、この問題は「平行四辺形の面積=合同な2つの三角形の面積の和」から考えることもできます。先ほどと同様に、三平方の定理により、三角形の高さを2 √3 と求めます。 よって、求める平行四辺形の面積は、1/2・5・2 √3 × 2 = 10 √3 です。

知識の「体系化」とは

このように、平行四辺形の面積を深掘りする(合同な2つの三角形の面積の和のように、より基本的な図形の面積の組み合わせに帰着させる)ことは、3. 活用のレベルに該当します(そこで三平方の定理が必要になったので、全体としては4. 総合のレベルです)。 このように、知識の「体系化」とは、数学のある知識(平行四辺形の面積公式)が、(三平方の定理を含めた)数学の知識のシステムに組み込まれているようにすることです。 「知識=識別を知ること」でした。他の知識との「違いは何か」「境目はどこか」「関係はどうか」といったことが整理されていることが重要です。知識はまた、「動的」なものであると認識することもきわめて重要です。 知識に完成はありません。出合うたび、利活用するたびに「しんか」させ続けていきましょう。 *　　　*　　　* 中学数学で解く大学入試問題 数学的思考力が驚くほど身につく画期的学習法 有名大学の問題が「解ける喜び」「考える楽しさ」を体感しよう！　中学数学の知識・技術で大学入試問題にトライして、数学の真髄に触れる。

杉山 博宣(岐阜県立高等学校教諭)

2/2ページ

【関連記事】