「覚えているだけ」では、ざんねんでしかない…「中学数学で大学入試を解く」のに「本当に必要」な知識レベル
東大や京大ほか、難関大学が出題した入試問題には、「数学の本質」がいっぱい詰まっている! 「よりすぐりの良問」を格好の素材として活用する新しい学習法を紹介した『中学数学で解く大学入試問題』が話題になっています。 中学数学の限られた知識や技術で、大学入試問題がなぜ解けるのか? どう解くのか? 思考過程を重視した素朴な解法を通して、有名大学の問題が「わかる喜び」「考える楽しさ」を体感すれば、「数学的思考力」が驚くほど身につく! *本記事は、『中学数学で解く大学入試問題 数学的思考力が驚くほど身につく画期的学習法』(ブルーバックス)を抜粋・再編集したものです。
「知識がある」といっても、レベルはさまざま
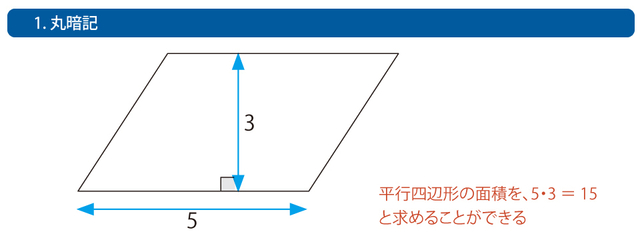
「知識がある」といっても、さまざまなレベルがあります。私は、次のように4分類しています。 丸暗記利用活用(応用・発展)総合 これらは明確に分類できるわけではありませんが、平行四辺形の面積に関する問題を例に、レベル分けしてみましょう。 次の平行四辺形の面積を、5・3=15と求めることができるのが、「1. 丸暗記」レベルの知識です。
丸暗記では「歯が立たない」問題
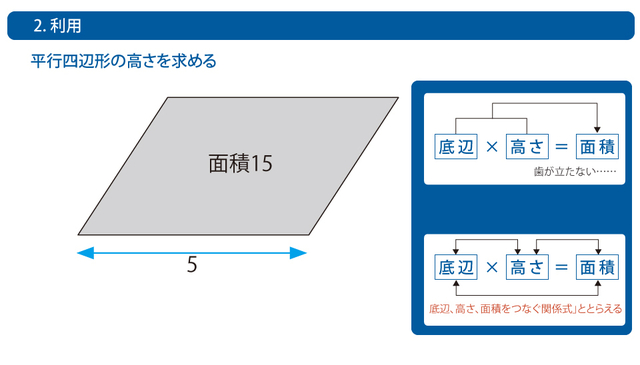
次の平行四辺形の高さを求める問題を、丸暗記で解くことができるでしょうか? 平行四辺形の「底辺×高さ=面積」という公式を、右上のように「左辺から右辺への一方通行の等式」ととらえていたのでは、この問題には歯が立ちません。 右下のように「底辺、高さ、面積をつなぐ関係式」ととらえることができ、求める高さをxとすると、5x=15と立式できます。 よって、高さx=3と求めることができるのが、「2. 利用」のレベルです。
不要な情報を見出せる「活用」のレベル
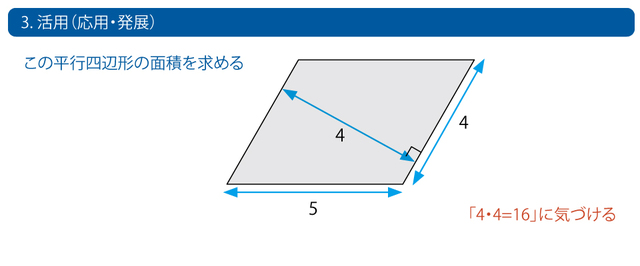
こんどは、次の平行四辺形の面積を求める問題です。 単に「底辺=下側の辺」ではなく、公式の意味まで理解して適切に利用でき、長さの5は不要であることがわかり、4・4=16 と面積を求めることができるのが、「3. 活用」のレベルです。 「2. 利用」と「3. 活用」の違いは、公式を 2.利用 字面(じづら)で理解している 3.活用 複眼的(今回は「数式+図形」的)に理解している ことです。2. 、3. には重なる部分もありますが、思考する(問題を解く)ことを通して、知識をしんかさせ、次の「4.総合」のレベルに到達しましょう。
【関連記事】
- 【続き】「中学数学で大学入試」問題に挑戦するなら、覚えておきたい…じつは「公式は証明から理解する」と、解ける問題が爆増する…その納得のワケ
- 東大も震撼した「円周率が3なんて、けしからん」…「計算力の低下問題」をはるかに超える問題「円が正六角形でいいんですか?」
- 中学数学なら「知っているはず」だけど、改めて問われると即答できない「1≦1は正しいですか」…大学入試で問われる「知識の質」
- 東大、京大の「出題意図」から見えてきた真実「じつは、大学は“知識”は問うていない」…「中学数学の大学入試問題」をわざわざ出題するわけ
- あの「東大の入試問題」は、日本社会に叩きつけた「問題提起」だったのかもしれない…良問にひそむ「数学教育界を揺るがす」衝撃のメッセージ