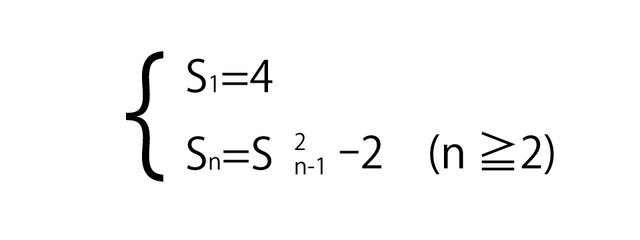photo by gettyimages

「素数シリーズ三部作」(『素数が奏でる物語』『素数はめぐる』『有限の中の無限』)でブルーバックスを代表する人気著者コンビ・西来路文朗さんと清水健一さん。最新刊『ガウスの黄金定理』も大好評のお二人が、新しい「数の世界」を案内してくださいます！ 今回は、今日11月11日にちなんで、「1が並ぶ数」にまつわるお話です。 先月、じつに6年ぶりに最大の素数が見つかるという数学界を盛り上げるビッグニュースが飛び込んできました。これまで最大だった素数を1600万桁以上も上回る、なんと4102万4320桁の数字だというのですから驚きです。 そしてさらに、こんな巨大な数が素数かどうかを判定する方法と、「1が並ぶ数」に深い関係があるというのですが、いったいどういうことなのでしょうか!?

52番目のメルセンヌ素数

「1だけが並ぶ数」の深すぎる世界を探訪した記事〈これが「ポッキー」ではなくて「1」に見えてしまったら、相当の数論好きかも…「1だけが並ぶ数」の深すぎる世界〉では、すべての桁が1である数「レピュニット数」の話から始めて、2進法のレピュニット数である「メルセンヌ数」についてご紹介しました。 「メルセンヌ数」が素数になる時って、どんな時…？　メルセンヌ数の不思議な世界が、もっとよくわかる前半は、こちらから それを受けて、「1だけが並ぶ数」の世界さらなる奥を探るこの記事では、メルセンヌ数2ⁿ－1の、nが素数pである場合を考えます。 メルセンヌ数2ᵖ－1は、pが 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, … の場合に素数になります。素数pに対して、2ᵖ－1が素数のときメルセンヌ素数とよばれています。 現在52個のメルセンヌ素数が見つかっていますが、52番目のメルセンヌ素数は先月発見されたばかりで、4102万4320桁にもおよぶ巨大な数字です。

素数かどうかをどう判定する？

写真:現代ビジネス

2ᵖ－1がメルセンヌ素数であるかどうかは、すぐにはわかりません。 2ᵖ－1がメルセンヌ素数であることを判定する方法に、リュカ・レーマーテストがあります。このテストは、フランスの数学者・リュカが1878年にメルセンヌ数の素数判定法を見出した後に、アメリカの数学者・レーマーが改良したものです。 で定義されるSₙに対し、 Sₚ₋₁が2ᵖ－1で割り切れる⇔2ᵖ－1は素数 が成り立ちます。先月の52番目のメルセンヌ数の発見にも、リュカ・レーマーテストが使われました。 たとえば、p=3のとき、2ᵖ－1=2³－1=7、p－1=2であり、 S₂=4²－2=14 となります。S₂が7で割り切れるので、7はメルセンヌ素数です。 p=5のとき、2ᵖ－1=2⁵－1=31、p－1=4であり、 S₂=4²－2=14 S₃=14²－2=194 S₄=194²－2=37634 となります。 37634=31×1214 より、S₄が31で割り切れるので、31はメルセンヌ素数です。