「中学数学で大学入試」問題に挑戦するなら、覚えておきたい…じつは「公式は証明から理解する」と、解ける問題が爆増する…その納得のワケ
「2で割った余り」による分類
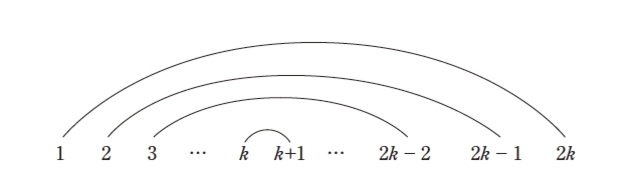
1:n=2k(k=n/2)のとき(kは自然数) kペアの2k+1ができるので、 1+2+…+n=1+2+…+2k =k(2k+1) k=n/2を代入すると、 =n/2{2・(n/2)+1} =n/2(n+1) =(1/2)n(n+1)
nが奇数のときで考えてみる
2:n=2k-1{k=(n+1)/2}のとき(kは自然数) k-1ペアの2kができ、kが1つ残るので、 1+2+…+n=1+2+…+2k-1 =(k-1)2k+k k=(n+1)/2を代入すると、 ={(n+1)/2-1}・2・{(n+1)/2}+{(n+1)/2} ={(n+1)/2-1}(n+1)+{(n+1)/2} ={(n+1)/2}(n+1)+{(n+1)/2} ={(n+1)/2}{(n-1)+1} =(1/2)n(n+1) 1:、2:のいずれの場合も、 1+2+……+n=(1/2)n(n+1) ところで、問題文には「和をnの多項式で示すこと」とありましたが、多項式とはなんでしょうか。
多項式で示すには
多項式とは、「いくつかの単項式の和として表される式」です。そのため、(1/2)n(n+1)で終わらずに、展開しておくとベターだと思います。 よって、 1+2+……+n=(1/2)n²+(1/2)n このような技法が、整数問題の技法「3. 余りで分類する」です。 今回はnの偶奇で分けて、ペアにして証明することができました。
理屈、理論から理解することの利点
今回の「1+2+…+n=(1/2)n(n+1)」のような重要な公式の証明には、多くの問題を解く際に有効なアイデアが詰まっています。そのため、公式は「証明」も含めて理解することを心がけましょう。 それにより、なぜその公式を使えば解けるのかを理解できると同時に、その「公式」と「証明のアイデア」の両者を応用問題にまで活用できるようになります。もちろん、「公式」と「証明」をセットで理解していることは、(活用とまではよべないレベルの)利用の精度を上げることにもつながります。 このように、「理屈、理論から理解することには、利点がある」ことを忘れてはいけません。 さて、続いては、数学における「実験」の大切さについてご説明しましょう。 * * * *次回は、11月22日(金)の公開予定です。 中学数学で解く大学入試問題 数学的思考力が驚くほど身につく画期的学習法 有名大学の問題が「解ける喜び」「考える楽しさ」を体感しよう! 中学数学の知識・技術で大学入試問題にトライして、数学の真髄に触れる。
杉山 博宣(岐阜県立高等学校教諭)