天才・ゲーデルの考えた「ゲーデル数」はなぜ必要か?そには「超数学」の視点が必要だった!【不完全性定理とはなにか】
上から目線で数学の全体像を眺める
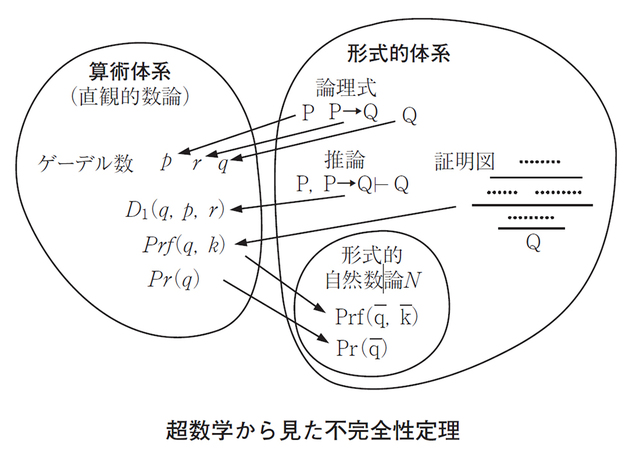
問題は、数学者が使う厳密な方法、すなわち、公理と推論規則を使って、どうやったら、数学自身について語ることができるか、である。こればかりは、どうしてもいったん数学の「外」に出て、上から目線で数学の全体像を眺めるよりほかない。 これが「超数学」だ。 「メタフィクション」という文学用語をご存じの読者は、「ああ、アレに似ているな」と気づかれたかもしれない。 メタフィクションでは、劇中劇のような状況が出現する。あるいは、あまり私は好きでないが、映画の最後に「すべて夢でした」という夢オチというのもある。フィクションの中にフィクションがあるのがメタフィクションだ。 数学そのものについて数学の方法で考えることは、フィクションの中でフィクションの手法を使うのと同じ構造なのである。
ゲーデルの発想と「超数学」
ゲーデルのやったことは、基本的には、数学におけるメタフィクションにほかならない。 メタフィクションは、理解しようとする人にしか理解できない。ちゃんと考えていないと、どのレベルの視点からストーリーを見ているのかがわからなくなり、レベルの混同が起こって、「こんなのつまらない!」と本を投げ出したり、上映途中で映画館を出たりするはめになる。 もちろん、メタフィクションの真骨頂は、意図的なレベルの混同にある。筒井康隆さんの作品が、かつて朝日新聞に連載されたとき、読者から「著者は頭がおかしいから連載を中止してほしい」という要望が寄せられた、という話を聞いたことがある。 実は、ゲーデルの証明には、意図的なレベルの混同が出てくる。なにしろ、算数では計算できないことがある、ということを、算数の計算で示してしまうんだから。この意味で、ゲーデルは稀代のサイエンス作家だったともいえる。
メタな視線で世界について考える
哲学によく出てくる「形而上学」(metaphysics)という言葉がある。あれも「物理世界」(physics)を超えて、メタな視線で世界について考えることを意味する。 しかし、あくまでも数学の方法論で考えないといけないので、この「メタ」な視点は空を飛び続けることはかなわず、地面に舞い降りてこなくてはならない。つまり、数学は、単に高みの見物というわけにはいかず、文字通り地に足の着いた数学の証明をする必要があるわけで、そのために、ゲーデル数による計算への落とし込みが必要になるのだ。 「メタな視点」、「ゲーデル数について語る」などと言われても実感がわかないかもしれない。こんな比喩はどうだろう。
銀行ではなぜ番号で呼ばれるのか?
大きな銀行に行くと、窓口で番号札を渡される。急いでいるあなたはイライラするけれど、もはやあなたは大塚さんでも竹内さんでもなく、28番と137番という数字に変換されてしまった。窓口の人は、あなたの人格や素性には興味がない。なぜなら、ここは金勘定が仕事の銀行なのだ。銀行というシステム内で客について語るためには「数字に変換する」のが一番。 なんだか、大手銀行への怨念が感じられる例で申し訳ないが、何か別のものに変換されてるんじゃないか、と感じることは現代社会ではよくある。あなた自身が数字に変換されていることが日常茶飯なのだから、算術の性質を数字に変換することで驚いていてはいけません。
竹内 薫(サイエンス作家)